library(Data4Ecologists) # for the clutch and gala data sets
library(splines) # spline basis functions for fitting non-linear relationships
library(ggplot2) # for plotting
theme_set(theme_bw()) # black and white background
library(gridExtra) # for producing multi-panel plots
library(ggthemes) # for additional ggplot palettes
library(dplyr) # for data wrangling 4 Modeling Non-linear relationships
Learning objectives:
Be able to model non-linear relationships between
- Polynomials using the
polyfunction in R - Linear regression splines using code you write yourself
- Cubic regression splines using the
nsfunction (splinespackage) - Smoothing splines (generalized additive models or GAMS).
- Polynomials using the
Understand how model predictions are constructed when using polynomials or splines.
4.1 R Packages
We being by loading several R packages:
In addition, we will use functions from:
ggeffectsfor creating effect plots illustrating non-linear relationshipsmgcvfor fitting generalized additive modelscarfor F-tests involving coefficients that code for non-linear effects
4.2 Modeling non-linear relationships
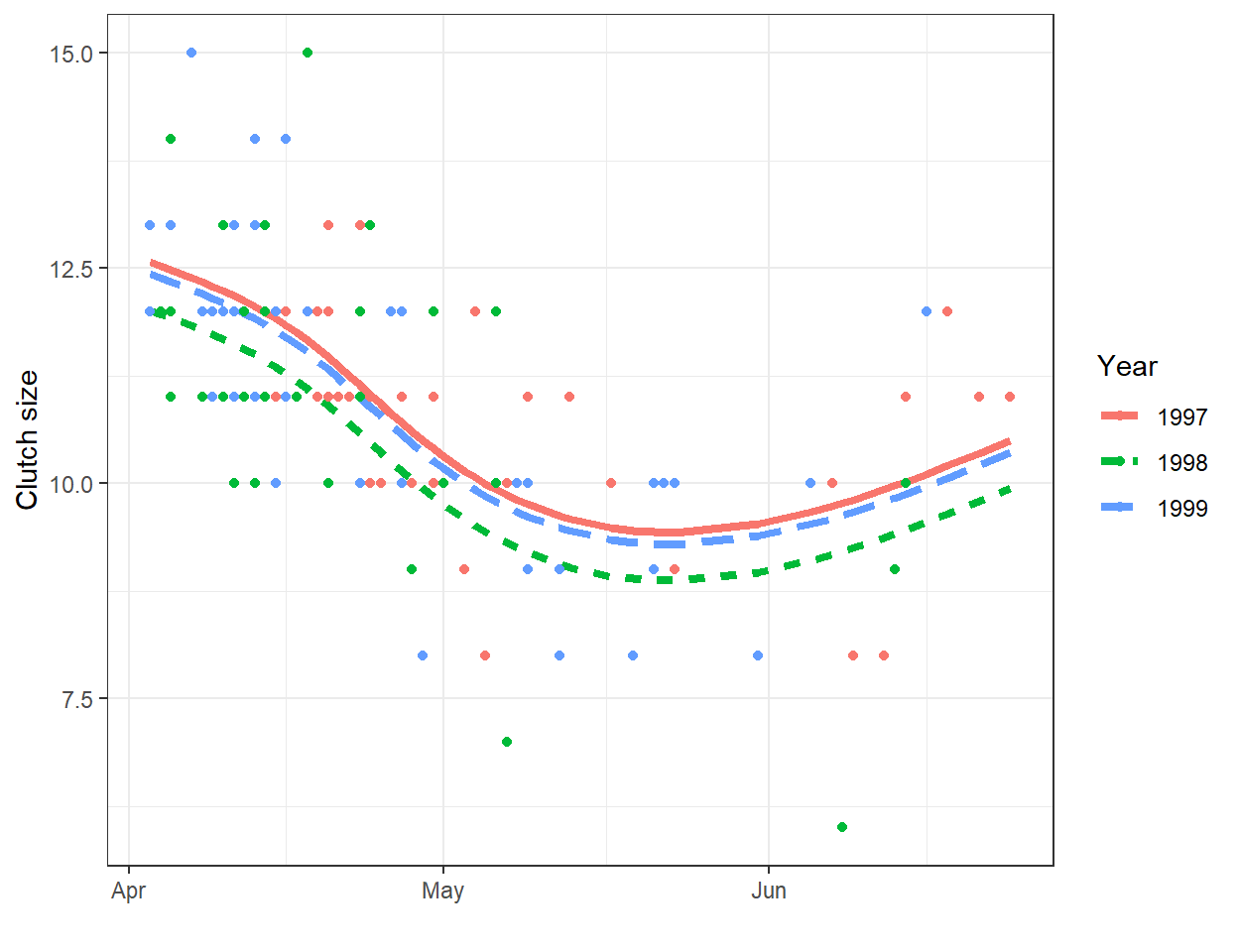
A line will often be useful for approximating the relationship between two variables over a given, potentially narrow range of data. However, most relationships are non-linear. As one example, consider the relationship between clutch size and Julian date from data collected on mallard ducks (Anas platyrhynchos) in Minnesota Figure 4.1. A line will nicely describe the relationship between clutch size and nest initiation date in early spring, but the relationship appears to change around the end of May.
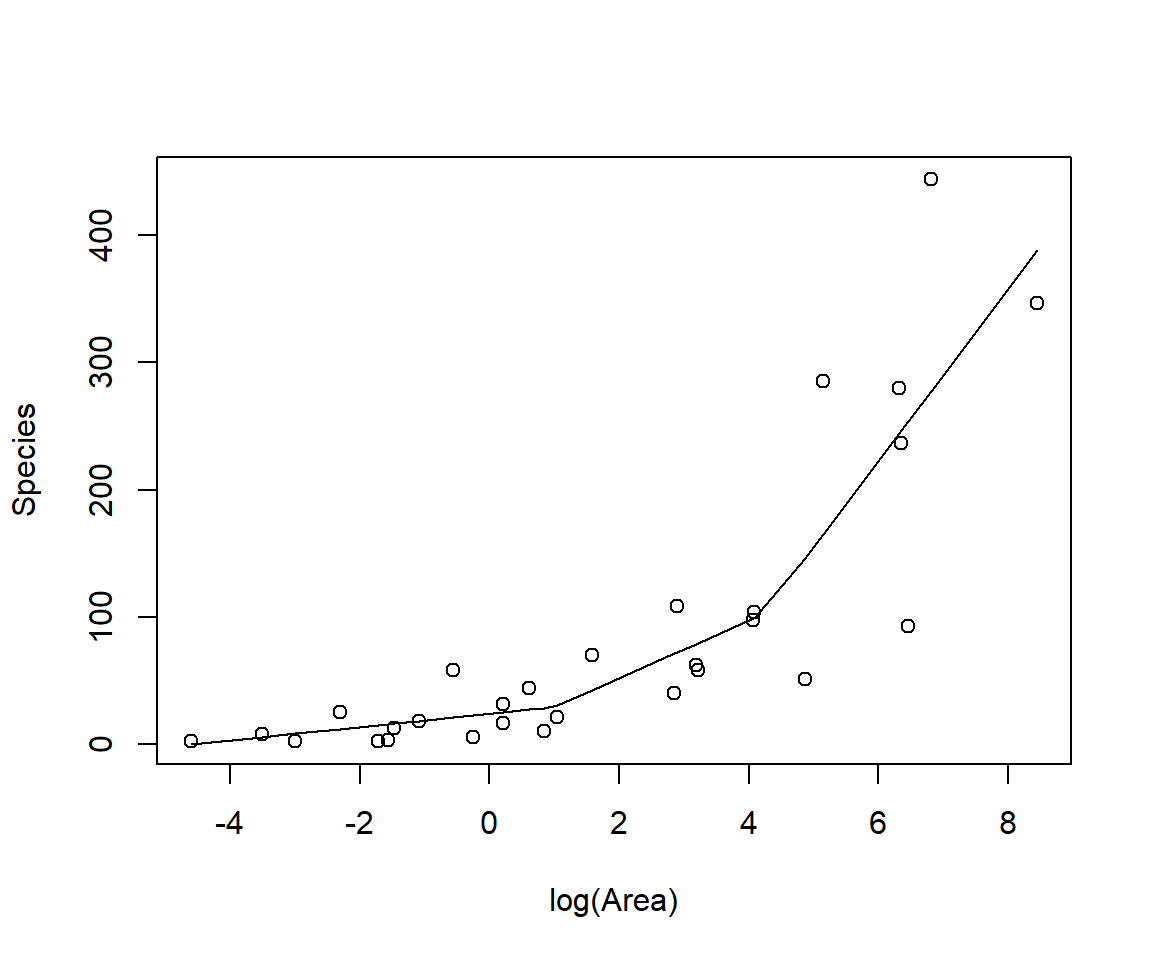
In the above example, the relationship between clutch size and nest initiation date was modeled using a polynomial, but other options are possible. To help understand different approaches to fitting non-linear relationships, we will begin by considering simple examples using data on plant species richness for 29 islands in the Galapagos Islands archipelago (Johnson and Raven 1973). This section borrows heavily from Jack Weiss’s lecture notes from his Statistical Ecology course (which unfortunately are no longer accessible), but also considers additional curve fitting approaches using polynomials and regression splines.
Ecologists have long been interested in how the number of unique species (
Let’s begin by plotting the data on plant species richness relative to area in a few different ways:
data(gala) # in Data4Ecologists package
gala$logarea<- log(gala$Area)p1 <- ggplot(gala, aes(x = Area, y = Species)) + geom_point(size = 3) +
xlab("Area")
p2 <- ggplot(gala, aes(x = logarea, y = Species)) + geom_point(size = 3) +
xlab("log(Area)")
p3<- ggplot(gala, aes(x = logarea, y = log(Species))) + geom_point(size = 3) +
xlab("log(Area)") + ylab("log(Species)")
gridExtra::grid.arrange(p1, p2, p3, ncol=3)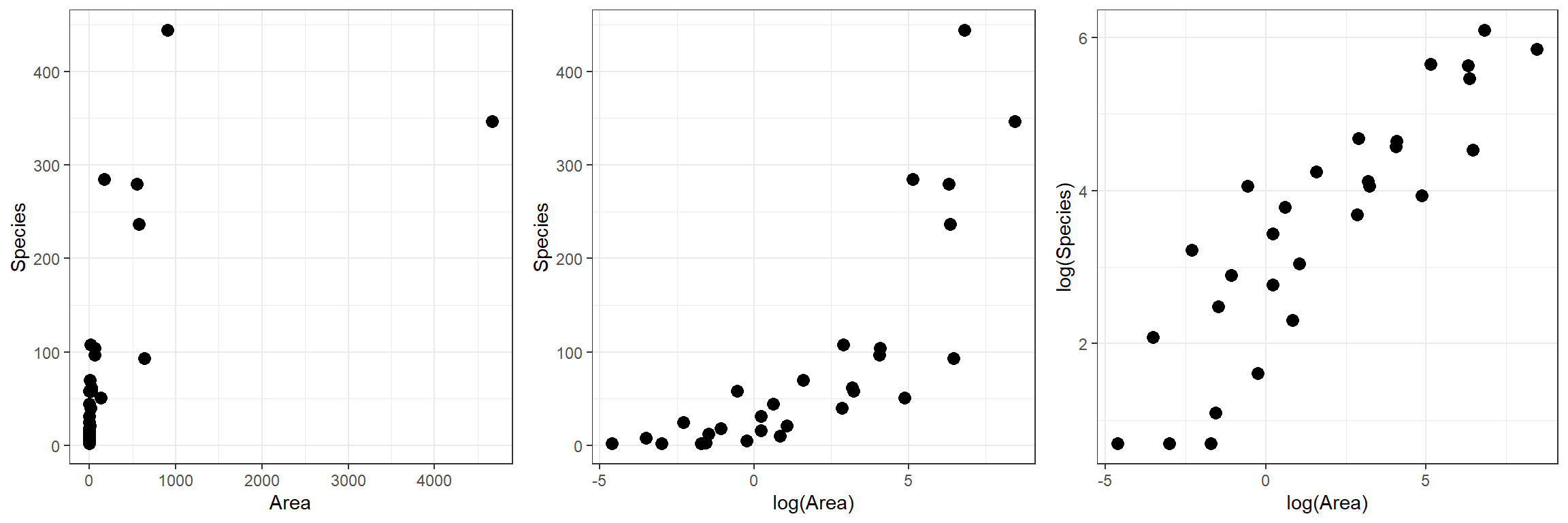
We clearly see that the first two models are not appropriate as the relationships between
lmloglog <- lm(log(Species) ~ log(Area), data=gala)
summary(lmloglog)
Call:
lm(formula = log(Species) ~ log(Area), data = gala)
Residuals:
Min 1Q Median 3Q Max
-1.44745 -0.40009 0.06723 0.51319 1.45385
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.83384 0.15709 18.040 < 2e-16 ***
log(Area) 0.40427 0.04121 9.811 2.13e-10 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.7578 on 27 degrees of freedom
Multiple R-squared: 0.7809, Adjusted R-squared: 0.7728
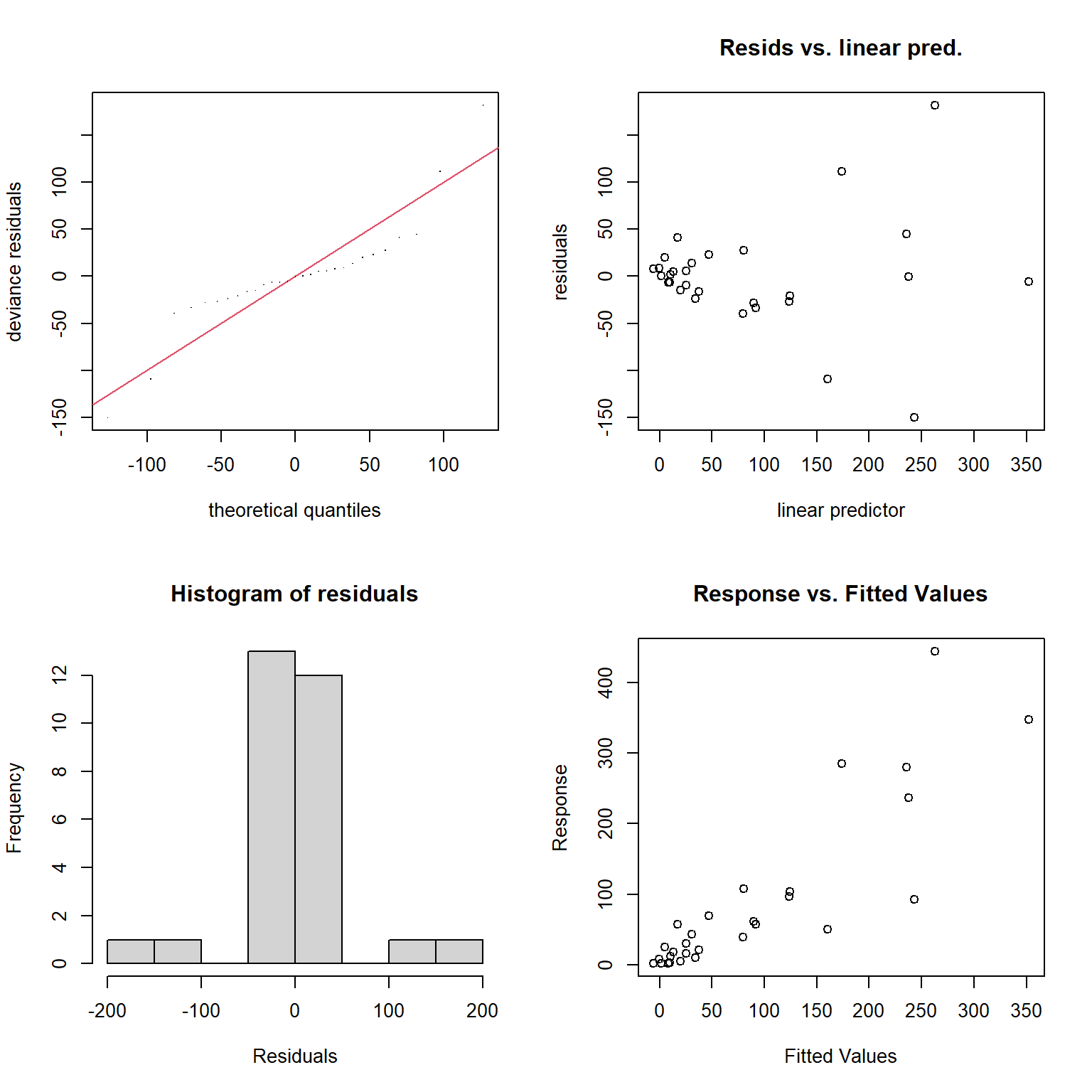
F-statistic: 96.25 on 1 and 27 DF, p-value: 2.135e-10performance::check_model(lmloglog,check = c("linearity", "homogeneity", "qq", "normality"))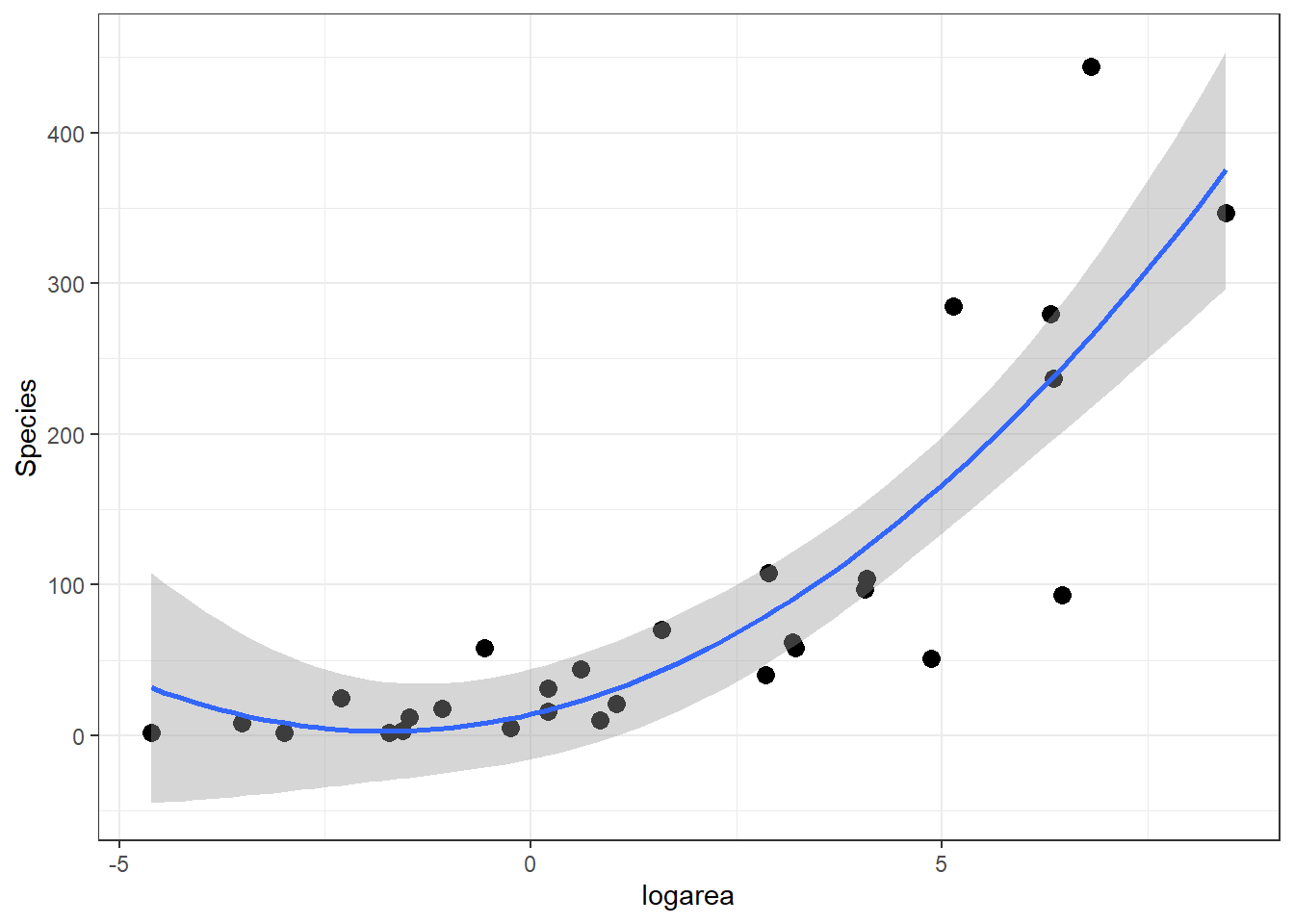
Everything looks OK, except for perhaps the constant variance assumption (i.e., the green line in the upper right panel of Figure 4.3 is not straight). Thus, we might conclude that this is a reasonable model for the data-generating process.
Importantly, this model is a linear model, but for the transformed response,
We can accommodate non-linear relationships within a linear models framework by using:
- Transformations of
- Polynomials (e.g.,including
- Splines or piecewise polynomials that are unique to different segments of the data
I.e., the following models are still technically “linear models” and can be easily fit using lm:
Thus, we can continue to use all the same diagnostic and inferential tools we learned about in Chapter 1 (e.g., residual plots, t-tests,
4.3 Polynomials
If we look at the relationship between Species and log(Area) (middle panel of Figure 4.2), it appears that a quadratic function might describe the mean species-area curve well. We can explore this model using ggplot by adding geom_smooth(method="lm", formula=y~poly(x,2), se=TRUE) (Figure 4.4).
ggplot(gala, aes(x=logarea, y=Species)) + geom_point(size=3)+
geom_smooth(method="lm", formula=y~poly(x,2), se=TRUE) 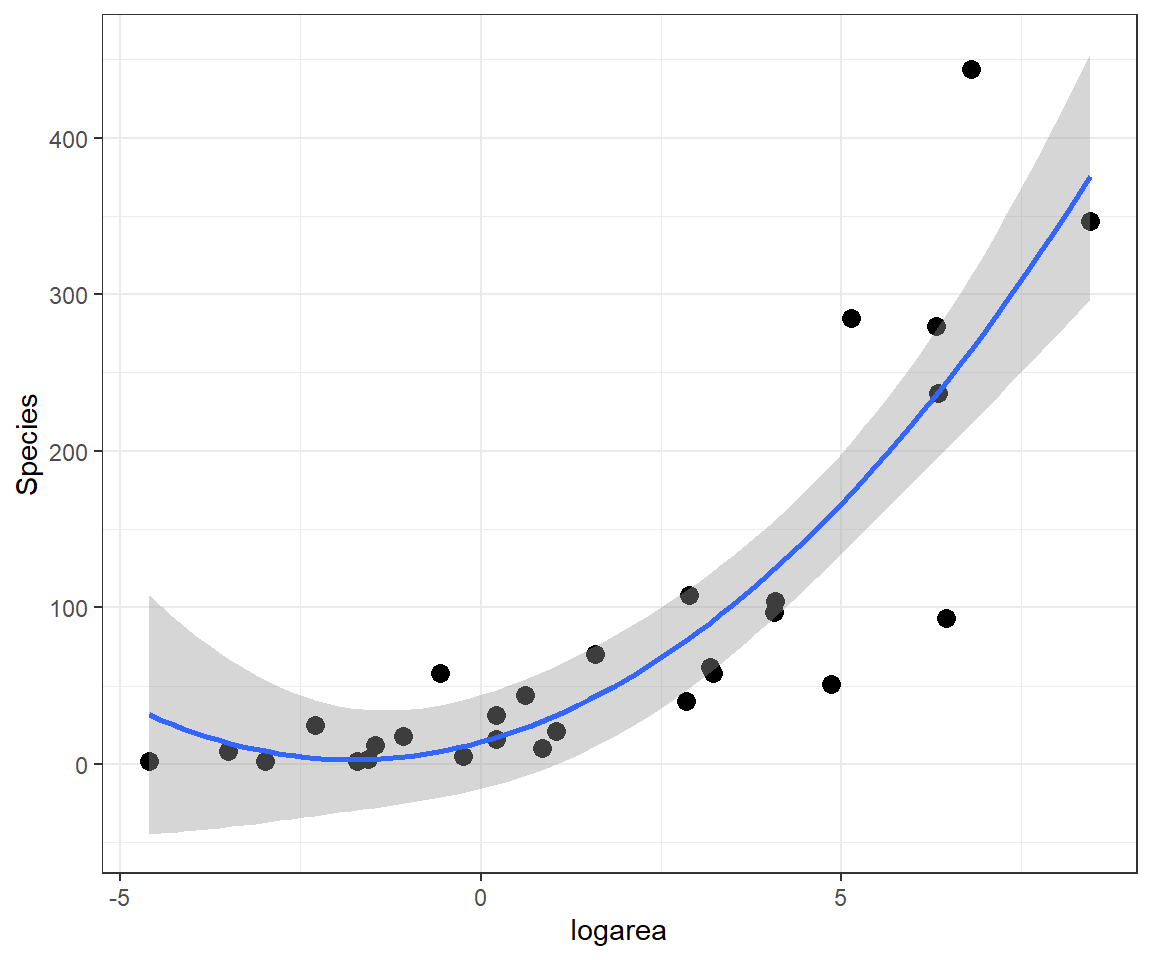
How can we fit this model using lm? One intuitive option would be to create a new “predictor” variable in our data set – the square of logarea and add this predictor to the linear model:
gala$logarea.squared <- gala$logarea^2
lm.poly <- lm(Species ~ logarea + logarea.squared, data = gala)
summary(lm.poly)
Call:
lm(formula = Species ~ logarea + logarea.squared, data = gala)
Residuals:
Min 1Q Median 3Q Max
-151.009 -27.361 -1.033 20.825 178.805
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 14.1530 14.5607 0.972 0.340010
logarea 12.6226 4.8614 2.596 0.015293 *
logarea.squared 3.5641 0.9445 3.773 0.000842 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 59.88 on 26 degrees of freedom
Multiple R-squared: 0.7528, Adjusted R-squared: 0.7338
F-statistic: 39.6 on 2 and 26 DF, p-value: 1.285e-08Think-Pair-Share: Write down equations for this model using matrix notation. Include the specific elements of the design matrix for the first few observations in the data set below:
head(gala, 3) Island Species Endemics Area Elevation Nearest.dist Santacruz.dist
1 Baltra 58 23 25.09 100 0.6 0.6
2 Bartolome 31 21 1.24 109 0.6 26.3
3 Caldwell 3 3 0.21 114 2.8 58.7
Adjacent.isl.area logarea logarea.squared
1 1.84 3.2224694 10.38430878
2 572.33 0.2151114 0.04627291
3 0.78 -1.5606477 2.43562139A better option would be to use R’s built in poly function within the call to lm.
lm.poly1.raw <- lm(Species ~ poly(logarea, 2, raw = TRUE), data = gala)
summary(lm.poly1.raw)
Call:
lm(formula = Species ~ poly(logarea, 2, raw = TRUE), data = gala)
Residuals:
Min 1Q Median 3Q Max
-151.009 -27.361 -1.033 20.825 178.805
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 14.1530 14.5607 0.972 0.340010
poly(logarea, 2, raw = TRUE)1 12.6226 4.8614 2.596 0.015293 *
poly(logarea, 2, raw = TRUE)2 3.5641 0.9445 3.773 0.000842 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 59.88 on 26 degrees of freedom
Multiple R-squared: 0.7528, Adjusted R-squared: 0.7338
F-statistic: 39.6 on 2 and 26 DF, p-value: 1.285e-08We get the exact same fit, but as we will see later, the advantage of this approach is that various functions used to summarize the model will know that logarea and its squared term “go together.” As such, we can more easily test for the combined linear and non-linear effect of logarea (e.g., using Anova in the car package), and we can construct a meaningful component + residual plot using termplot (see e.g., Section 4.11 for more on constructing models using polynomial terms and an explanation of what the argument raw = TRUE is doing).
4.4 Basis functions/vectors
Let’s dig deeper to see what is going on under the hood in our polynomial model:
We see that our predicted response,
More generally, we can write any linear model as a sum of parameters
The logarea (Hefley et al. 2017). Our polynomial model can be written in terms of 3 basis vectors logarea (our
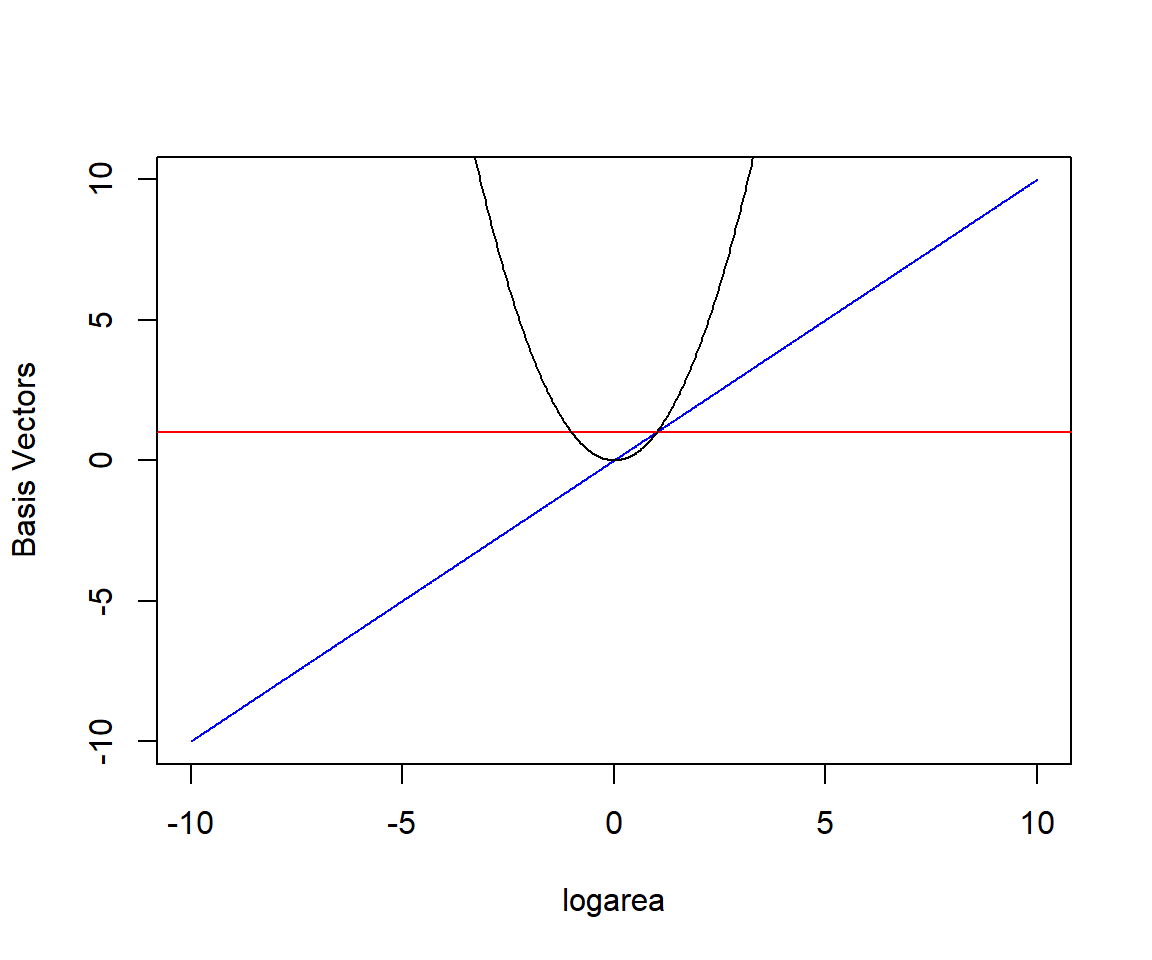
Let’s look at our design matrix using model.matrix for the first 6 observations and also the first 6 values of logarea.
head(model.matrix(Species~ poly(logarea,2, raw=TRUE), data=gala)) (Intercept) poly(logarea, 2, raw = TRUE)1 poly(logarea, 2, raw = TRUE)2
1 1 3.2224694 10.38430878
2 1 0.2151114 0.04627291
3 1 -1.5606477 2.43562139
4 1 -2.3025851 5.30189811
5 1 -2.9957323 8.97441185
6 1 -1.0788097 1.16383029gala$logarea[1:6][1] 3.2224694 0.2151114 -1.5606477 -2.3025851 -2.9957323 -1.0788097We see that poly created two variables in our design matrix, logarea and logarea*logarea.
Our predicted species richness at any given value of logarea,
In other words,
More generally, a model with polynomial of degree D in
Specific polynomials:
- Linear:
- Quadratic:
- Cubic:
The design matrix for a regression model with
Higher order polynomials can allow for more complex patterns, but they have “global constraints” on their shape. For example, quadratic functions must eventually either increase (or decrease) as
Splines allow us to gain further flexibility by combining polynomials applied separately to short segments of our data along with local constraints that ensure the different polynomials get “stitched” together in a reasonable way.
4.5 Splines
Splines are piecewise polynomials used in curve fitting. They may seem mysterious at first, but like polynomials, they can be understood as models that weight different basis vectors constructed from predictor variables included in the model.
4.5.1 Linear splines
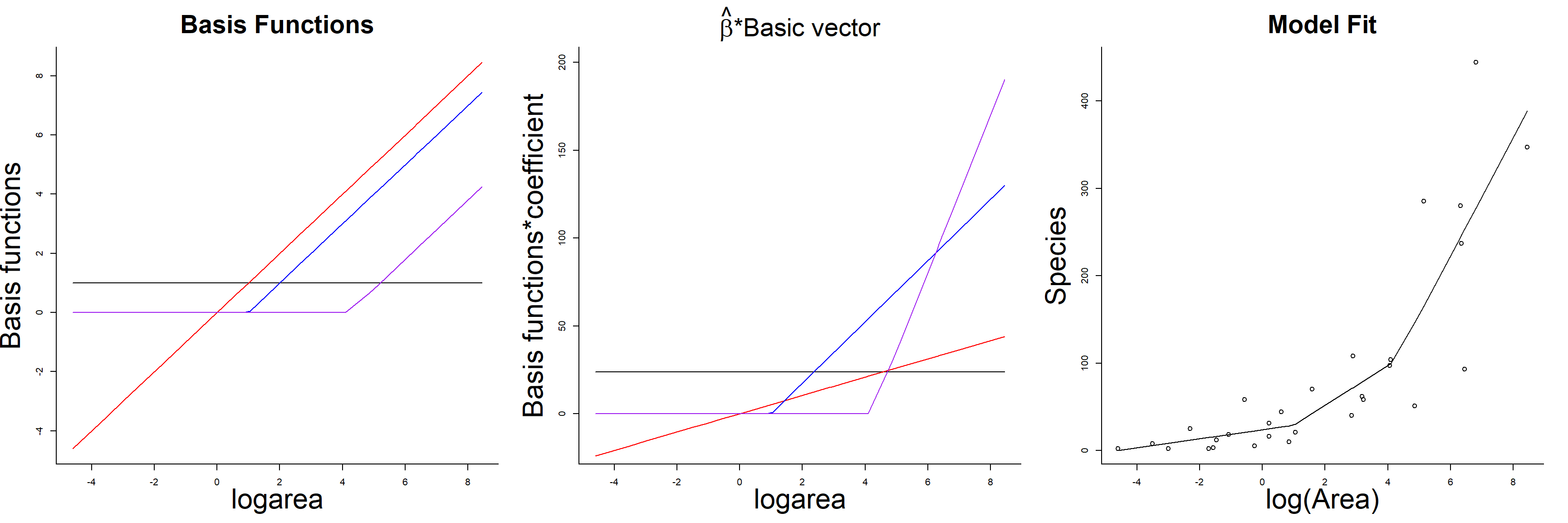
Linear models are often a good approximation over small ranges of
The above plot was constructed by fitting a model with the effect of logarea modeled using a linear spline. A linear spline is a continuous function formed by connecting linear segments. The points where the segments connect are called the knots of the spline.
We chose 2 knots (located at logarea = 1 and 4.2, where the relationship between Species and logarea appeared to change) and formed two basis vectors by subtracting the knot from logarea and setting the value to 0 whenever the expression was negative:
(logarea-1)(logarea-4.2)
where the
gala$logarea<- log(gala$Area)
gala$logarea.1<- ifelse(gala$logarea<1, 0, gala$logarea-1)
gala$logarea.4.2<- ifelse(gala$logarea<4.2, 0, gala$logarea-4.2) We then fit our model using lm:
lm.sp<-lm(Species~logarea+logarea.1+logarea.4.2, data=gala)
summary(lm.sp)
Call:
lm(formula = Species ~ logarea + logarea.1 + logarea.4.2, data = gala)
Residuals:
Min 1Q Median 3Q Max
-160.691 -16.547 -4.209 13.133 166.430
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 23.869 17.384 1.373 0.1819
logarea 5.213 8.956 0.582 0.5658
logarea.1 17.464 18.836 0.927 0.3627
logarea.4.2 44.815 23.156 1.935 0.0643 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 58.97 on 25 degrees of freedom
Multiple R-squared: 0.7695, Adjusted R-squared: 0.7418
F-statistic: 27.82 on 3 and 25 DF, p-value: 3.934e-08As with the polynomial model, our predicted species richness at any given value of logarea,
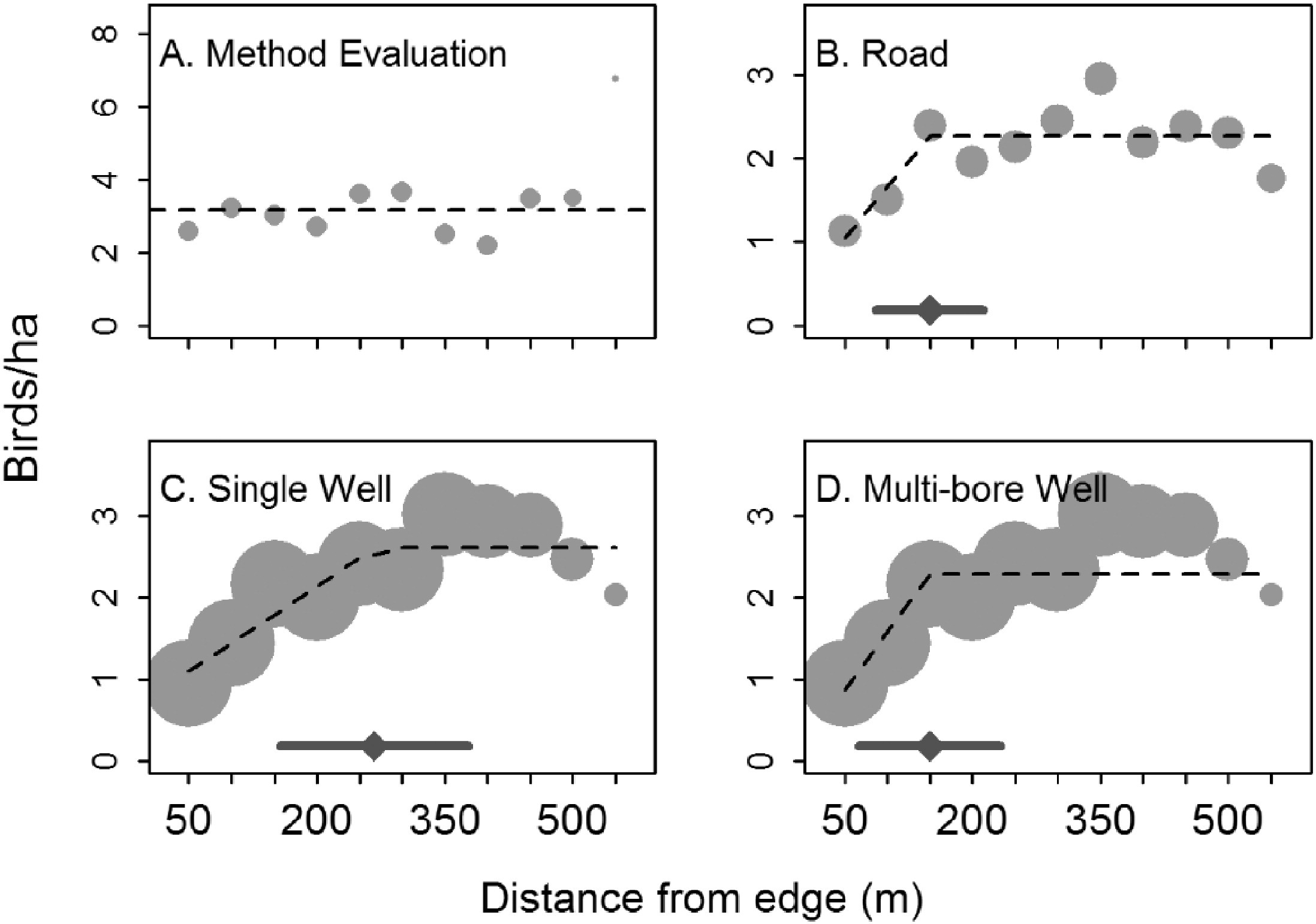
Linear splines can sometimes be useful for modelling abrupt changes in response variables or to depict relationships where we might expect a response variable to asymptote after crossing some threshold value of the predictor variable. For example, Thompson et al. (2015) used linear splines with a constraint that the slope be 0 after a single knot to model the effect of disturbance from oil and gas wells on bird abundance (Figure 4.8). In general, however, we often prefer to allow for smoother trends compared to the abrupt changes that result from using linear splines.
4.5.2 Cubic regression splines
Linear splines (D = 1) only ensure our function is continuous. The first derivative, which describes if the function is increasing or decreasing, is not constant. As a result, our fitted curve (Figure 4.6) looks somewhat jagged at the knot locations. In fact, the fitted model can be increasing before a knot and decreasing after it! Usually, we expect biological relationships to be smoother than this. Therefore, unless we have an expectation that
We can model non-linear relationships by connecting polynomial segments of degree D such that:
- the function is continuous (i.e., it is not disjointed when it hits a knot)
- the function has D-1 continuous derivatives
- the D
Cubic splines (D = 3) are commonly used in model fitting, and ensure that
There are a number of different ways of creating basis vectors that lead to piecewise cubic polynomials with continuous first and second derivatives. The simplest approach is to use truncated polynomials, which is how we created our linear spline. We can create a truncated polynomial basic vector of degree D associated with a knot location
We could then fit a model that includes these basis vectors:
The design matrix for a cubic spline with
Although truncated power bases are relatively easy to understand and construct, they may lead to numerical problems due to scaling issues (Perperoglou et al. 2019). Other popular options are:
- B-splines, which can be constructed using the
bs(x, df=)function insplinespackage - Natural or restricted cubic splines constructed using the
ns(x, df=)function insplinespackage
B-splines are numerically more stable than those based on the truncated power basis but can be poorly behaved near the edge of the data range. Natural or restricted cubic splines address this problem by assuming the model is linear before the first knot and after the last knot. A further advantage of these additional constraints is that it requires fewer basis vectors and thus, fewer model degrees of freedom than B-splines with the same number of knots. We will return to this point when we get to the section on model selection (Chapter 8).
In addition to b-splines and natural splines, cyclical splines can be used to model circular data like time of day or annual response patterns (e.g., Ditmer et al. 2015). In these cases, we would want our model to give similar predictions just before versus just after midnight or just before versus after a new year begins. Cyclical splines use basis vectors that are formed in a way that ensures these constraints are upheld.
4.5.3 Natural cubic regression splines
To fit a model with the effect of logarea on species richness modeled using a natural cubic regression spline, we use the ns function in the splines package. Using the second argument, df, we can specify the degrees of freedom that we want to use when modeling the effect of the predictor. This will equate to the number of coefficients estimated in the model.
lm.ns <- lm(Species ~ ns(logarea, df = 3), data = gala)
summary(lm.ns)
Call:
lm(formula = Species ~ ns(logarea, df = 3), data = gala)
Residuals:
Min 1Q Median 3Q Max
-156.173 -13.819 -5.998 13.922 170.555
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.468 43.542 0.034 0.9734
ns(logarea, df = 3)1 47.790 45.957 1.040 0.3084
ns(logarea, df = 3)2 276.125 102.146 2.703 0.0122 *
ns(logarea, df = 3)3 381.743 45.084 8.467 8.22e-09 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 59.48 on 25 degrees of freedom
Multiple R-squared: 0.7655, Adjusted R-squared: 0.7374
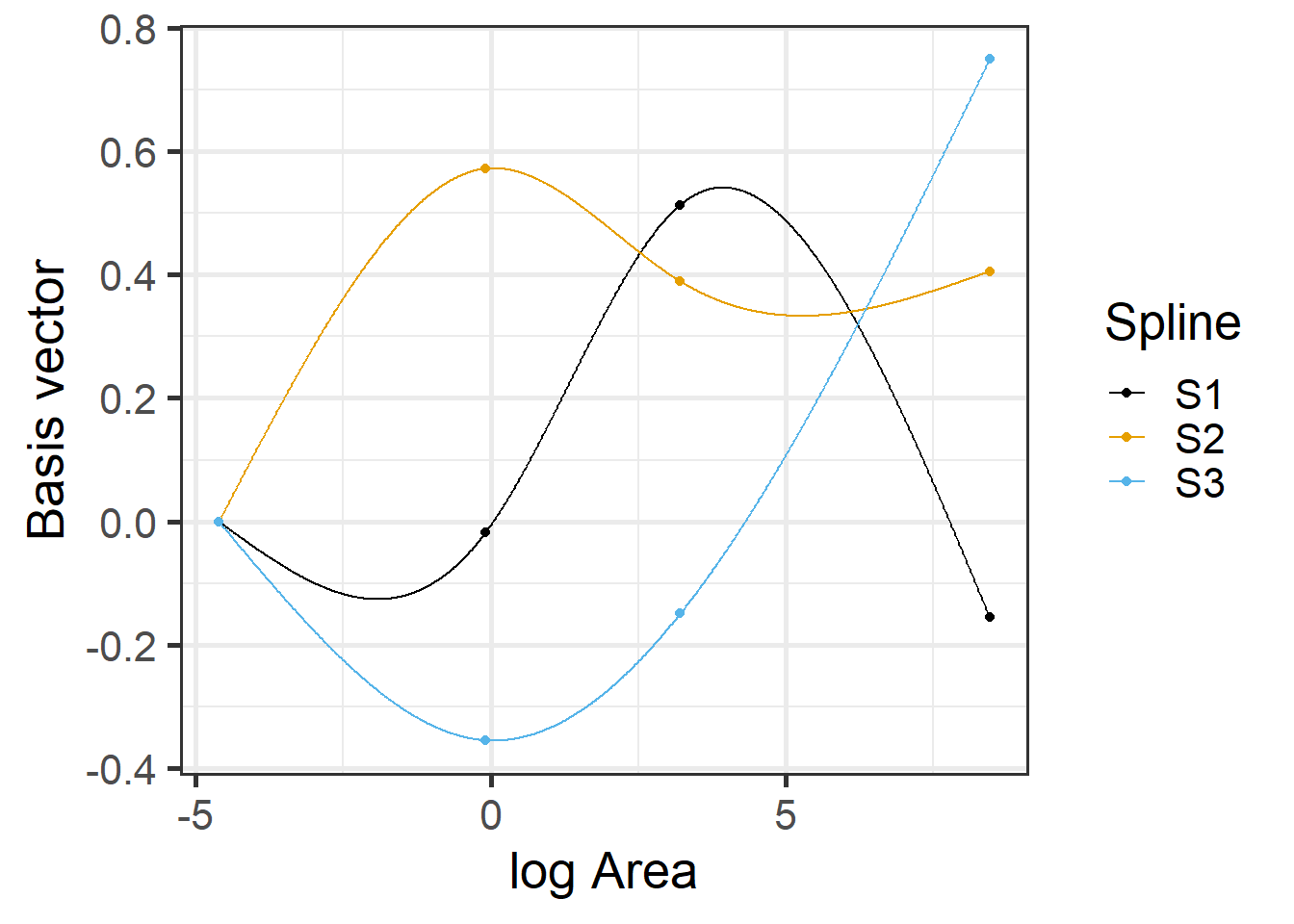
F-statistic: 27.21 on 3 and 25 DF, p-value: 4.859e-08We see from the output that we have estimated an intercept and 3 coefficients associated with logarea. Let’s look at the design matrix for the first few observations and a plot of the different basis functions created by ns (i.e., the columns of the design matrix) versus logarea (Figure 4.9 (a)).
head(model.matrix(lm.ns)) (Intercept) ns(logarea, df = 3)1 ns(logarea, df = 3)2 ns(logarea, df = 3)3
17 1 0.00000000 0.0000000 0.0000000
8 1 -0.07289332 0.1993098 -0.1235349
5 1 -0.09952908 0.2856200 -0.1770311
4 1 -0.12204050 0.3907838 -0.2422131
9 1 -0.12443447 0.4653235 -0.2884138
3 1 -0.12199115 0.4821792 -0.2988612The predicted species richness values are again formed by weighting the basis functions in Figure 4.9 along with the intercept. We can use ggplot to see the resulting fitted curve (Figure 4.10).
ggplot(gala, aes(x = logarea, y = Species)) + geom_point(size = 3) +
geom_smooth(method = "lm", formula = y ~ ns(x, df = 3), se = TRUE) 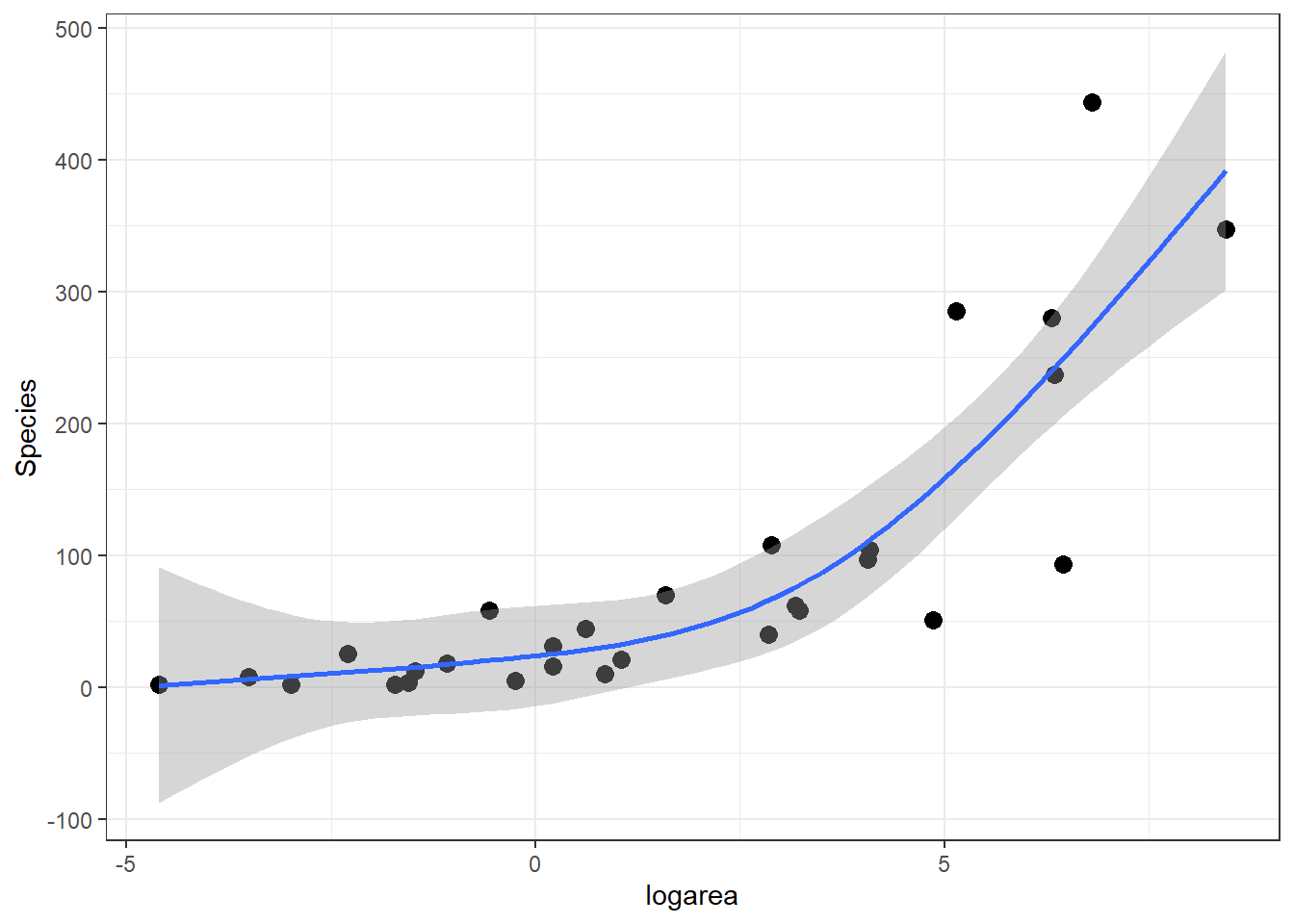
4.5.4 Number of knots and their locations
The shape of a spline can be controlled by carefully choosing the number of knots and their exact locations in order to allow greater flexibility where the trend appears to be changing quickly, while avoiding overfitting in regions where the trend changes little. We could, in principle, compare models (e.g., using AIC) that have varying numbers of knots, or different knot locations. The danger here is that we would open the door to a wide range of possible models, increasing the chances we would overfit our data. Further, proper accounting of model-selection uncertainty associated with such data-driven processes can be challenging, a topic we will discuss in Chapter 8.
An alternative strategy is to choose a small number of knots (df), based on how much data you have and how complex you expect the relationship to be a priori (Harrell Jr 2015). I have personally found that 2 or 3 internal knots are usually sufficient for small data sets. Also, Keele and Keele (2008), cited in Zuur et al. (2009), recommend 3 knots if ns does by default if you do not provide knot locations). Fortunately, models fit with cubic regression splines are usually not too sensitive to knot locations (Harrell Jr 2015). Alternatively, you can choose to place knots in places where you expect the relationship between
We can see the knots chosen by ns using:
attr(ns(gala$logarea,3), "knots")[1] -0.09393711 3.20877345attr(ns(gala$logarea,3), "Boundary.knots")[1] -4.605170 8.448769The first set of knots are often referred to as internal knots, whereas the latter set of knots are located at the outer limits of the data (remember, the model is assumed to be linear outside of this range):
range(gala$logarea)[1] -4.605170 8.4487694.6 Splines versus polynomials
We have not yet talked about how we can compare competing models, but one popular method is to use the Akaike’s Information Criterion or AIC (Akaike 1974; Anderson and Burnham 2004). Smaller values of AIC are generally preferable.
lmfit <- lm(Species ~ logarea, data = gala)
AIC(lmfit, lm.poly1.raw, lm.sp, lm.ns) df AIC
lmfit 3 335.1547
lm.poly1.raw 4 324.4895
lm.sp 5 324.4646
lm.ns 5 324.9600# lmfit = linear model
# lm.poly1.raw = model with quadratic
# lm.sp = linear spline model
# lm.ns = cubic regression spline modelHere, we see that all of the non-linear approaches we have so far considered fit better than a linear model. Although the natural cubic regression spline and polynomial models have similar AIC values, the spline model seems to provide a better fit for especially small values of logarea (Figure 4.11). In particular, the polynomial model appears to suggest species richness will stop decreasing and actually start increasing once logarea decreases past a certain point and approaches the smallest values in our data set, which does not seem reasonable. This is an inherent limitation of quadratic polynomials, which all have to eventually point in the same direction at the extremes of the data. By contrast, splines offer more “local control” when fitting deviations from linearity.
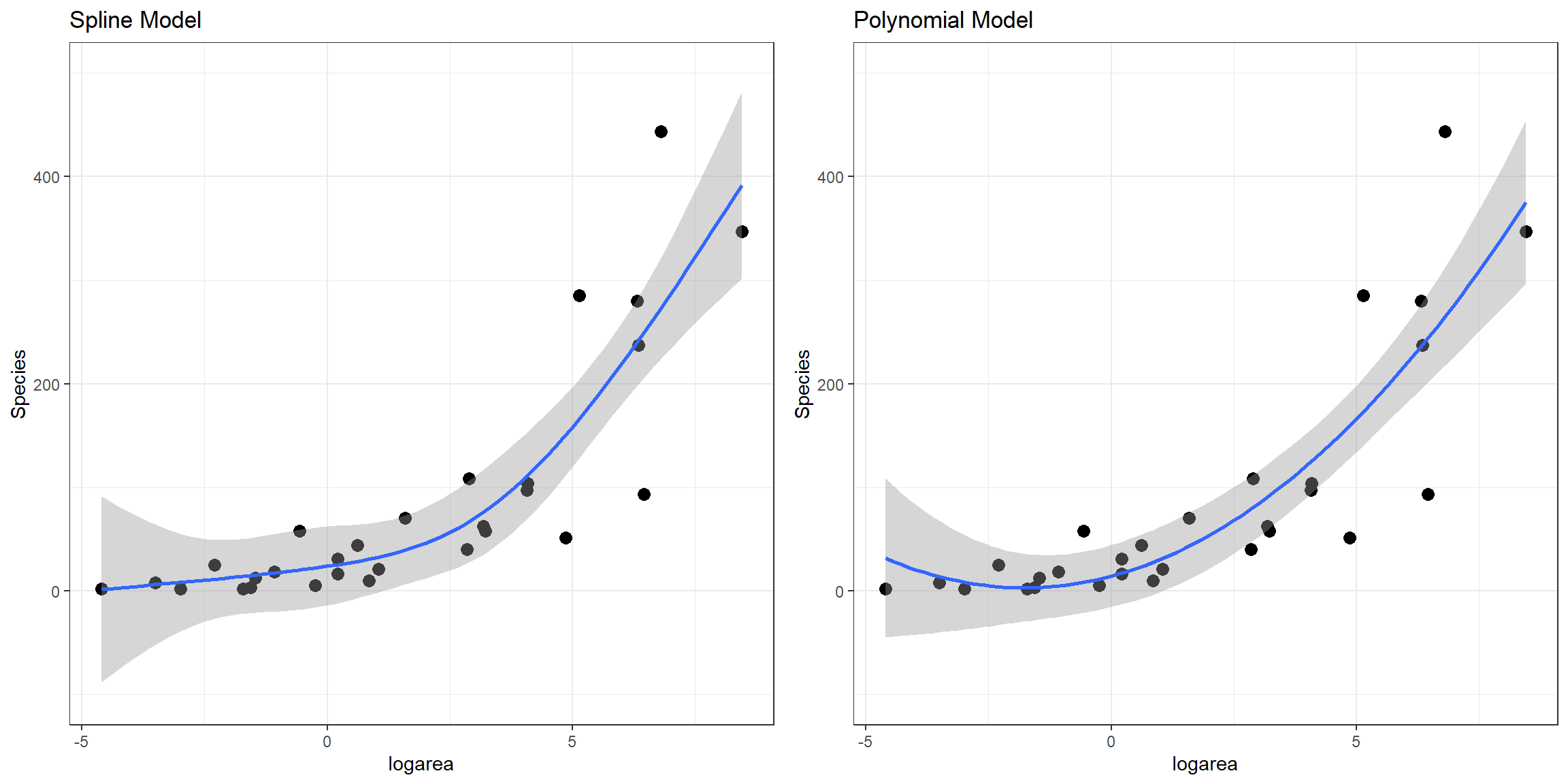
4.7 Visualizing non-linear relationships
In the previous sections, we used ggplot to visualize our fitted models (e.g., Figure 4.10). This worked since our model only included a single predictor, logarea. More generally, we can use termplot to create a partial residual plot (see Section 3.14.2) depicting the effect of logarea while controlling for other predictors that may be included in the model:
termplot(lm.ns, se = T, partial = T, pch = 16, main = "Partial Residual Plot")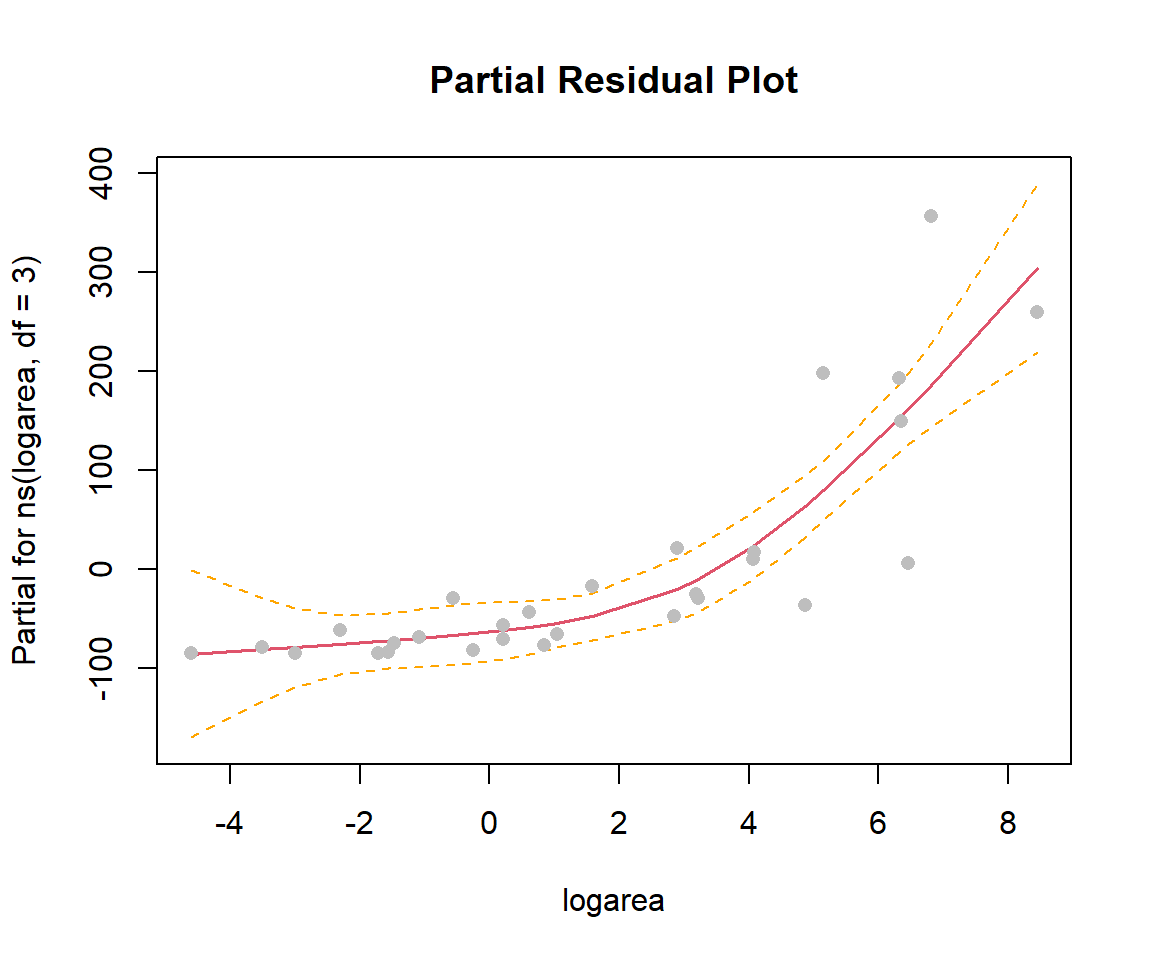
logarea on species richness in the natural cubic regression spline model fit to plant species richness data collected from 29 islands in the Galapagos Islands archipelago. Data are from Johnson and Raven (1973).
Another option is to use the ggeffects package (Lüdecke 2018) to produce effect plots (see Section 3.14.3; Figure 4.13).
library(ggeffects)
plot(ggpredict(lm.ns, terms = "logarea"), show_residuals = TRUE)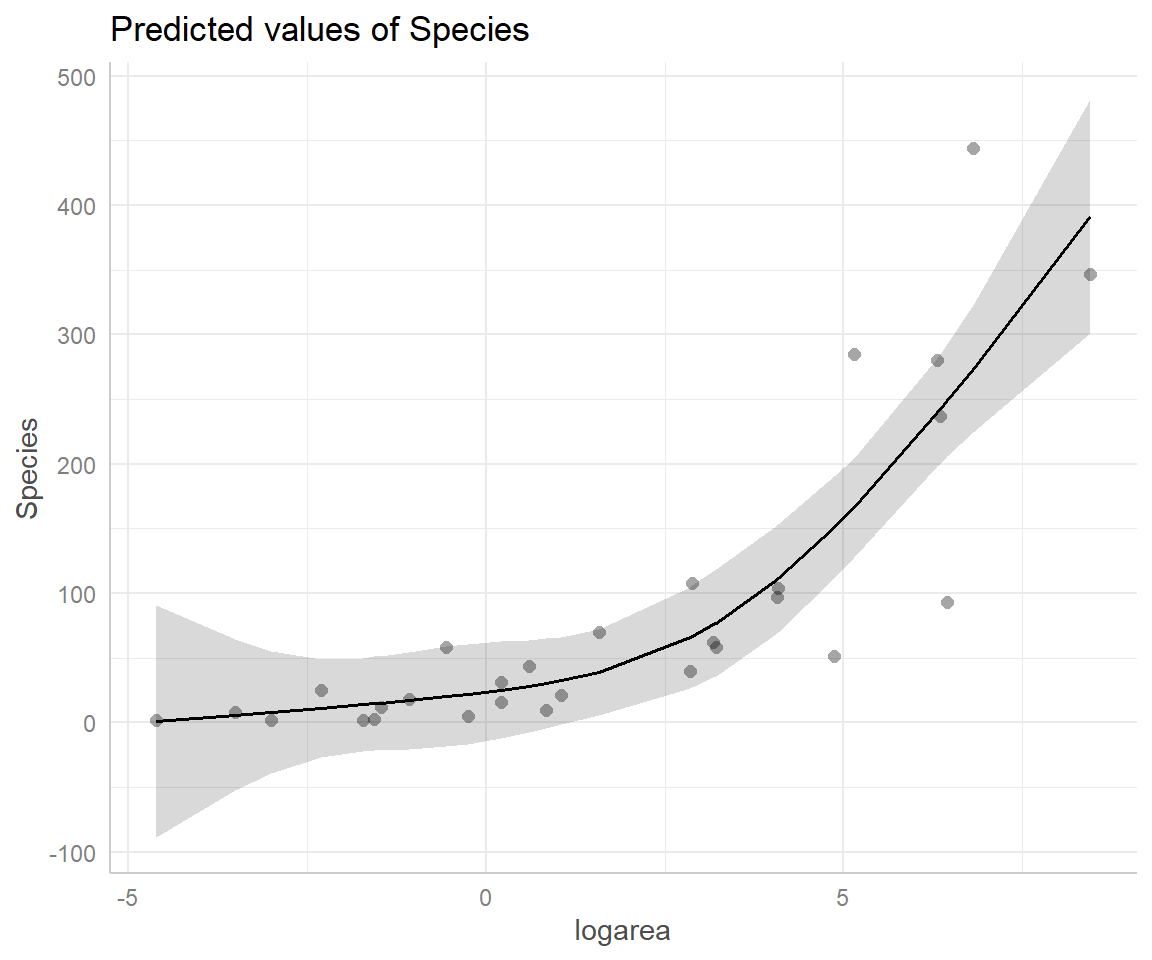
logarea on species richness in the natural cubic regression spline model fit to plant species richness data collected from 29 islands in the Galapagos Islands archipelago. Data are from Johnson and Raven (1973).
4.8 Generalized additive models (GAMS)
In general, non-linear models, including those that we have discussed so far with a single predictor, can be described via the following equation:
where
Here,
In this framework, how should we determine
where
We can fit a GAM model, allowing for a non-linear relationship between species richness and log(Area) using the gam function in mgcv package (S. N. Wood 2004; S. N. Wood 2017):
library(mgcv)
sfit <- gam(Species ~ s(logarea), data = gala)
summary(sfit)
Family: gaussian
Link function: identity
Formula:
Species ~ s(logarea)
Parametric coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 87.34 11.11 7.864 2.76e-08 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Approximate significance of smooth terms:
edf Ref.df F p-value
s(logarea) 2.465 3.107 24.86 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
R-sq.(adj) = 0.734 Deviance explained = 75.8%
GCV = 4062.7 Scale est. = 3577.3 n = 29The small p-value for s(logarea) tells us that there is a relationship between logarea and Species and the associated edf tells us that this relationship required approximately 2.5 effective model degrees of freedom (edf) to describe it accurately. Note, however, because GAMs use the data to choose
To understand the model, it is best to explore the fit of the model using the associated plot function.
plot(sfit, scheme=1)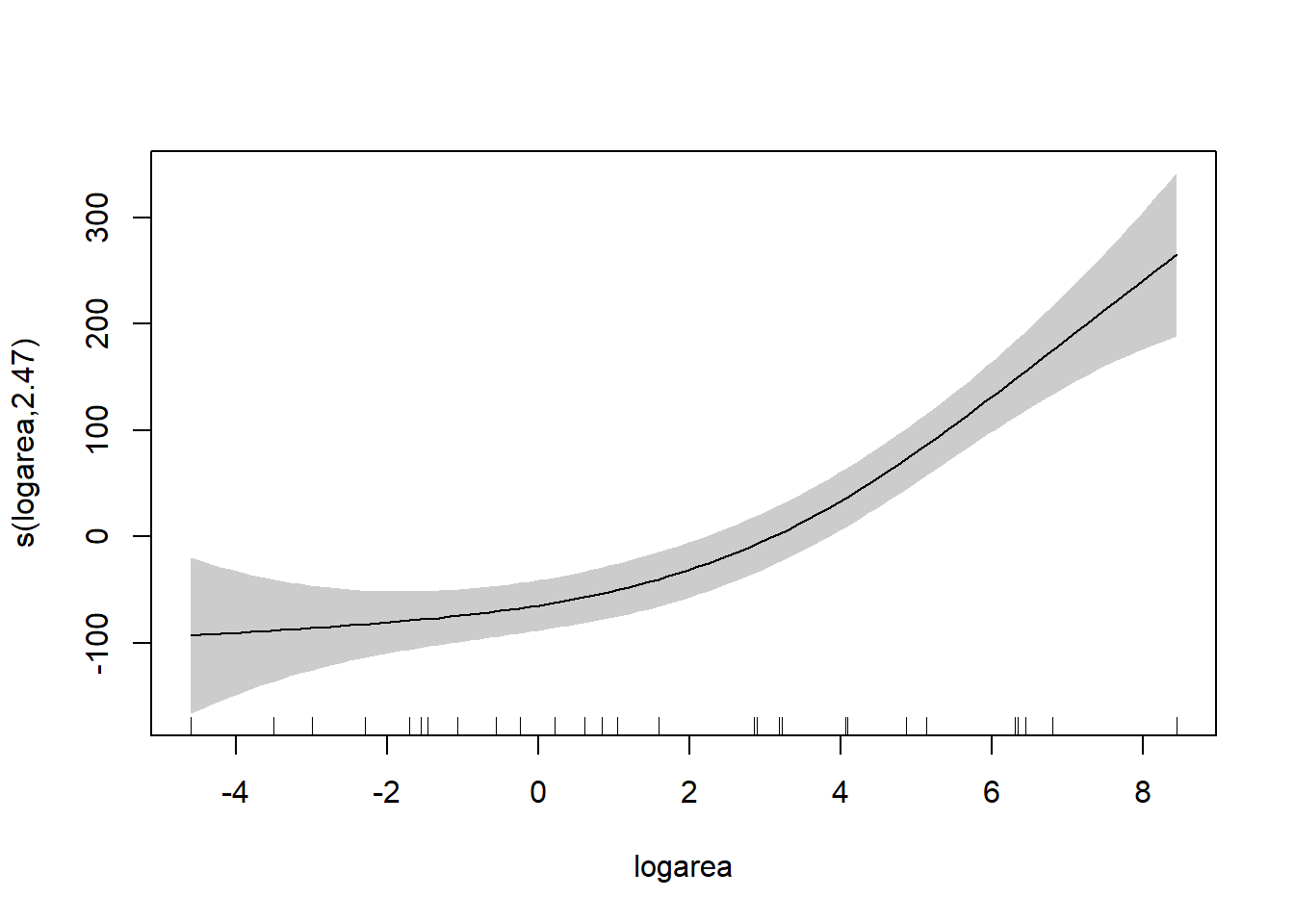
mgcv package (S. N. Wood 2004; S. N. Wood 2017). Data are from (Johnson and Raven 1973).
Besides the assumption of linearity, which we have relaxed, we otherwise have the same distributional assumptions as in any linear regression model, namely, that errors are normally distributed with constant variance. We can use the gam.check function to explore whether these assumptions are met.
par(mfrow=c(2,2))
gam.check(sfit)
Method: GCV Optimizer: magic
Smoothing parameter selection converged after 6 iterations.
The RMS GCV score gradient at convergence was 0.0002855077 .
The Hessian was positive definite.
Model rank = 10 / 10
Basis dimension (k) checking results. Low p-value (k-index<1) may
indicate that k is too low, especially if edf is close to k'.
k' edf k-index p-value
s(logarea) 9.00 2.47 1.43 0.98The plots produced by the gam.check function (Figure 4.15) suggest that the error variance increases with
As mentioned previously, the model is fit by creating a large number of basis vectors and then estimating the coefficients for those basis vectors using the penalized sum of squares in Equation 4.2. The large p-value associated with the “Basis dimension check” suggests that the default choice for number of basis vectors (9 here) was sufficient for modeling the relationship between logarea and Species. If this p-value is small, then we would want to use more knots. If you are interested in learning more about GAMS, we highly recommend Noam Ross’s online and free GAM class.
4.9 Generalizations to multiple non-linear relationships
What if you want to allow for multiple non-linear relationships? We can add multiple ns terms to our model or use multiple smoothing splines (see Zuur et al. 2009, chap. 3; S. N. Wood 2017). We could also consider other basis functions to fit smooth surfaces (allowing for interactions between variables), including tensor splines, thin plate splines, etc… (see S. N. Wood 2017). It is also possible to include interactions with regression splines or to allow each level of a categorical variable to have its own smooth when using smoothing splines (see Zuur et al. 2009, chap. 3).
4.10 Non-Linear models with a mechanistic basis
Sometimes we may have a theoretical model linking
- The Ricker model for stock-recruitment:
- A typical predator-prey relationship:
Some of these models can be fit using non-linear least squares in R (e.g., using the nls function in base R). Alternatively, we will eventually learn how to fit custom models using Maximum likelihood and Bayesian methods (see Section 10.7).
4.11 Aside: Orthogonal polynomials
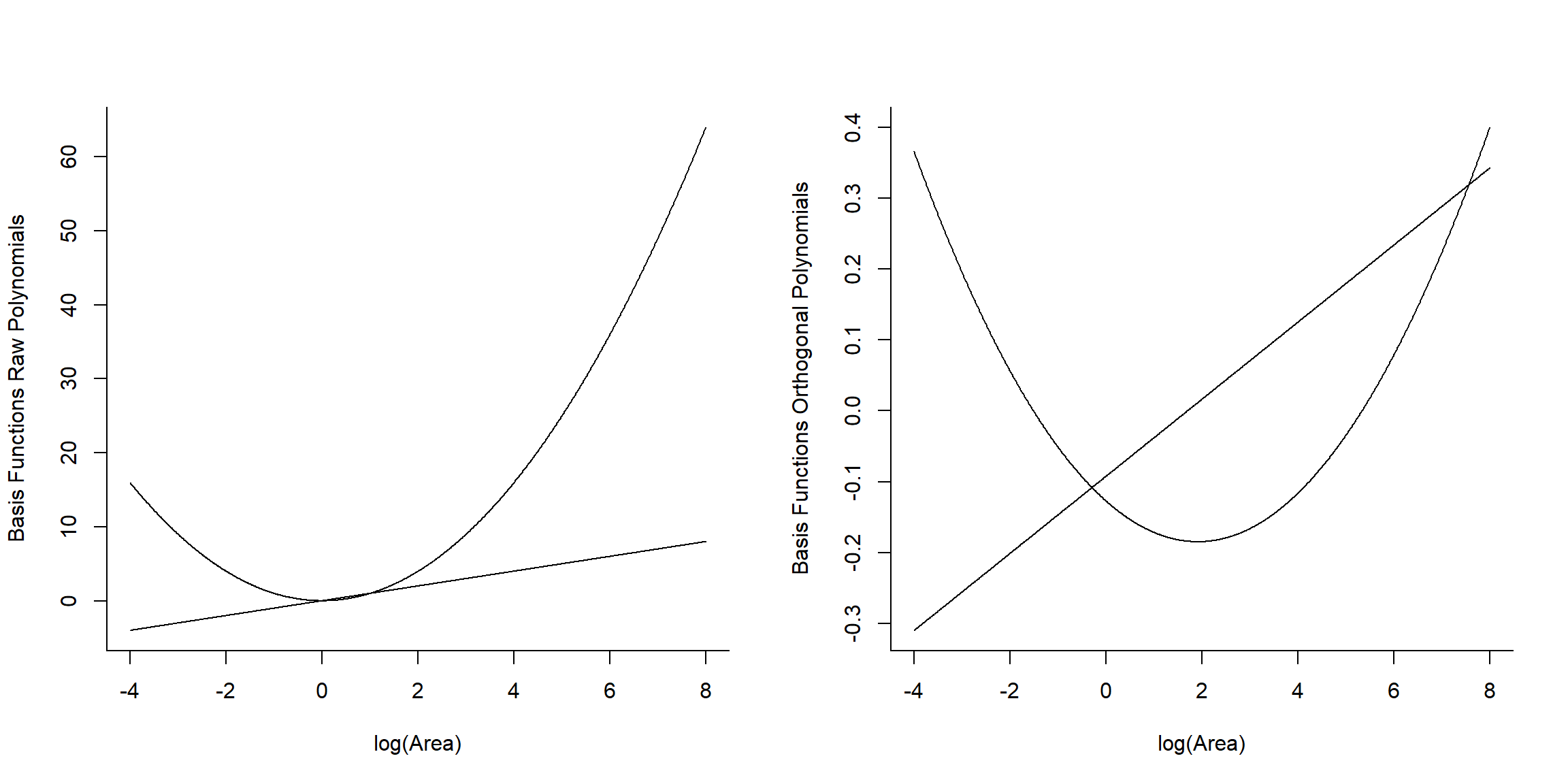
Standard polynomial-basis vectors can cause numerical issues when fitting linear models due to differences in scale. For example, if
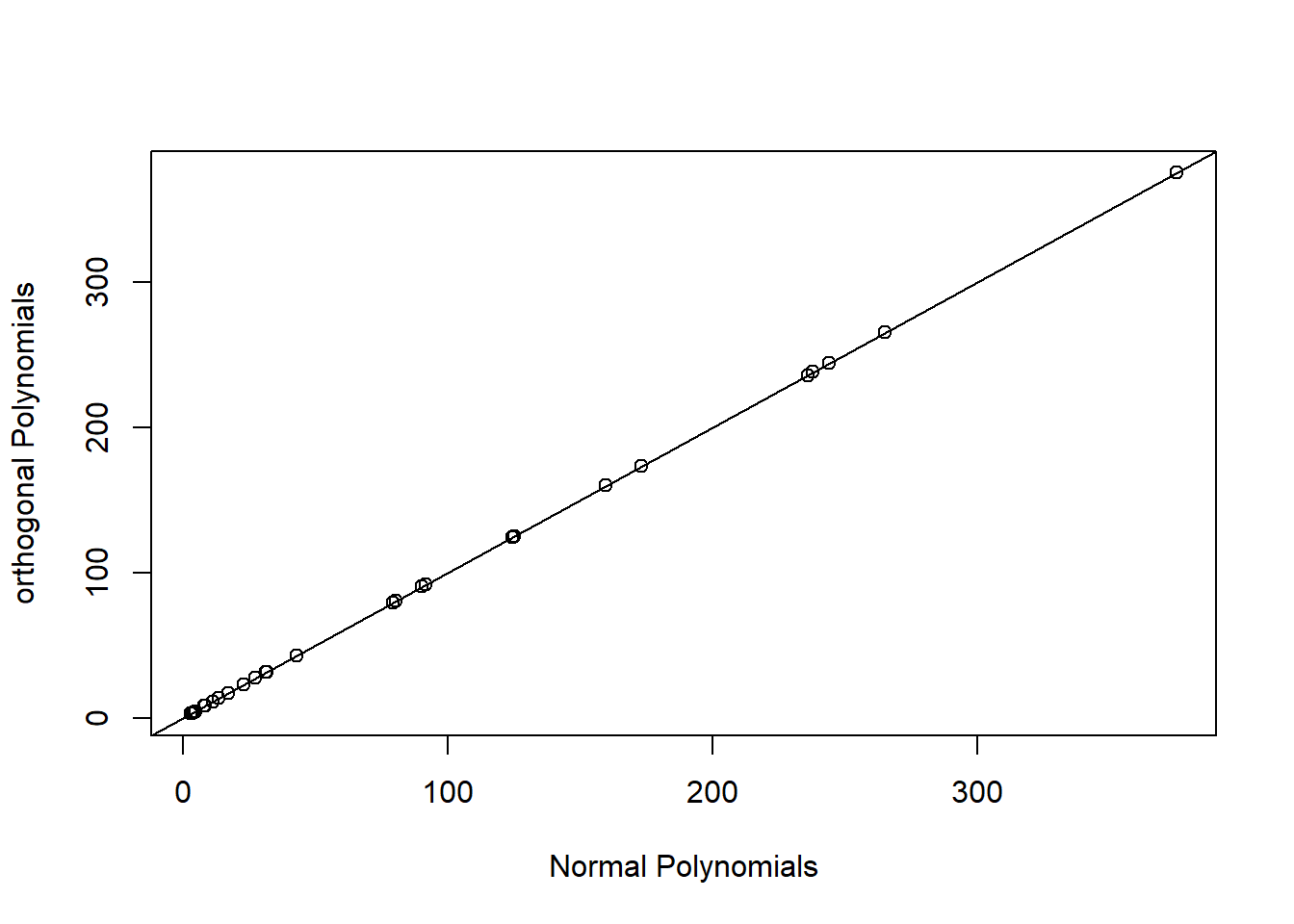
Alternatively, we can use orthogonal polynomials created using poly(raw=FALSE) (the default). This will create a different set of basis functions for fitting a quadratic polynomial, but one that leads to an identical fit as the raw polynomial model. We can verify this by comparing predicted values and statistical tests for the effect of logarea modeled with both raw and orthogonal polynomials (Figure 4.16).
lm.poly.raw<-lm(Species~poly(logarea,2, raw=TRUE), data=gala)
lm.poly.orth<-lm(Species~poly(logarea,2), data=gala)
plot(fitted(lm.poly.raw), fitted(lm.poly.orth), xlab="Normal Polynomials",
ylab="orthogonal Polynomials")
abline(0,1).
library(car)
Anova(lm.poly.raw) #log(Area)+ I(log(Area)^2)Anova Table (Type II tests)
Response: Species
Sum Sq Df F value Pr(>F)
poly(logarea, 2, raw = TRUE) 283970 2 39.596 1.285e-08 ***
Residuals 93232 26
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Anova(lm.poly.orth) # poly(logarea,2)Anova Table (Type II tests)
Response: Species
Sum Sq Df F value Pr(>F)
poly(logarea, 2) 283970 2 39.596 1.285e-08 ***
Residuals 93232 26
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Let’s look at the basis vectors used to model the effect of logarea in the two models (Figure 4.17):
head(poly(gala$logarea,2), 3) 1 2
[1,] -0.3425801 0.4850314
[2,] -0.2828395 0.2782420
[3,] -0.2550617 0.1950582head(cbind(gala$logarea, gala$logarea^2),3) [,1] [,2]
[1,] -4.605170 21.207592
[2,] -3.506558 12.295948
[3,] -2.995732 8.974412We see that raw and orthogonal polynomials use different basis vectors. Both sets of vectors span the set of all quadratic polynomial functions, meaning that we can form any quadratic polynomial using a weighted sum of either set of basis vectors (for more, see Hefley et al. 2017). So, while they result in different parameter estimates, the models and fitted values are identical!
4.12 Aside: Segmented and piecewise regression
Segmented and piecewise regression offer a similar approach to splines in that one can construct models by splicing together polynomials fit to different segments of predictor space, but with the knots treated as free parameters that are to be estimated from the data (Toms and Lesperance 2003; Wolfson, Andersen, and Fieberg 2022). Although we won’t cover these methods here, these models can be fit in a frequentist or Bayesian framework, e.g., using either the segmented (Muggeo et al. 2014) or mcp (Lindeløv 2020) packages in R, respectively.