9 Introduction to probability distributions
Learning objectives
Understand and be able to work with basic rules of probability. We will need these rules to understand Bayes Theorem, which is fundamental to Bayesian statistics.
Gain a basic familiarity with concepts related to mathematical statistics (e.g., random variables, probability mass and density functions, expected value, variance, conditional and marginal probability distributions).
Understand how to work with different statistical distributions in R.
Understand the role of random variables and common statistical distributions in formulating modern statistical regression models.
Be able to choose an appropriate statistical distribution for modeling your data.
9.1 Statistical distributions and regression
Up until now, our focus has been on linear regression models, which can be represented as:
Moving forward, we are going to use the last formulation to emphasize the role of the Normal distribution as our data-generating model. This formulation allows us to easily see that we are:
- Modeling the mean,
- The Normal distribution describes the variability of the observations about
The Normal distribution has several characteristics that make it a poor data generating model for certain types of data (e.g., count or binary data):
- the distribution is bell-shaped and symmetric
- observations can take on any value between
In this chapter, we will learn about other statistical distributions and ways to work with them in R. Along the way, we will learn about discrete and continuous random variables and their associated probability mass functions (discrete random variables) and probability density functions (continuous random variables). We will also learn a few basic probability rules that can be useful for understanding Bayesian methods and for constructing models using conditional probabilities (e.g., occupancy models; MacKenzie et al. 2017).
9.2 Probability rules
We will begin by highlighting a few important probability rules that we will occasionally refer back to:
- Multiplicative rule:
- Union:
- Complement rule:
- Conditional probability rule:
If you forget these rules, it is often helpful to create a visualization using a Venn diagram (i.e., an illustration with potentially overlapping circles representing different events). For example, consider the Venn diagram representing numbers between 1 and 10 along with whether the numbers are prime and whether they are even (Figure 9.2).
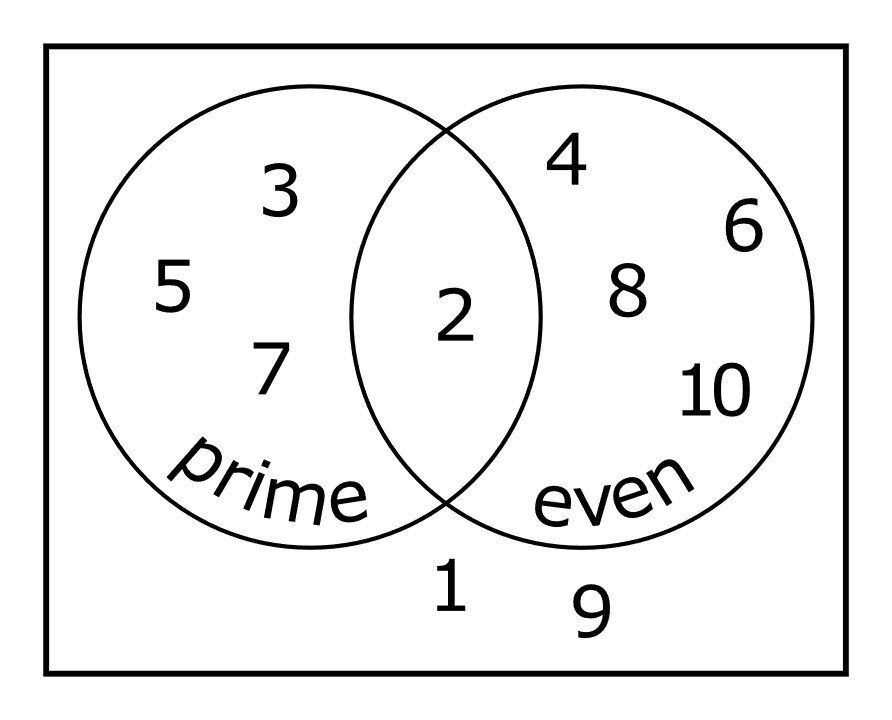
Let
It is also helpful to know of two special cases having to do with mutually exclusive or independent events. If events A and B are mutually exclusive (meaning that they both cannot happen), then:
If events A and B are independent:
Lastly, it will be helpful to know the Law of Total Probability (Figure 9.3). If we partition the sample space into a set of
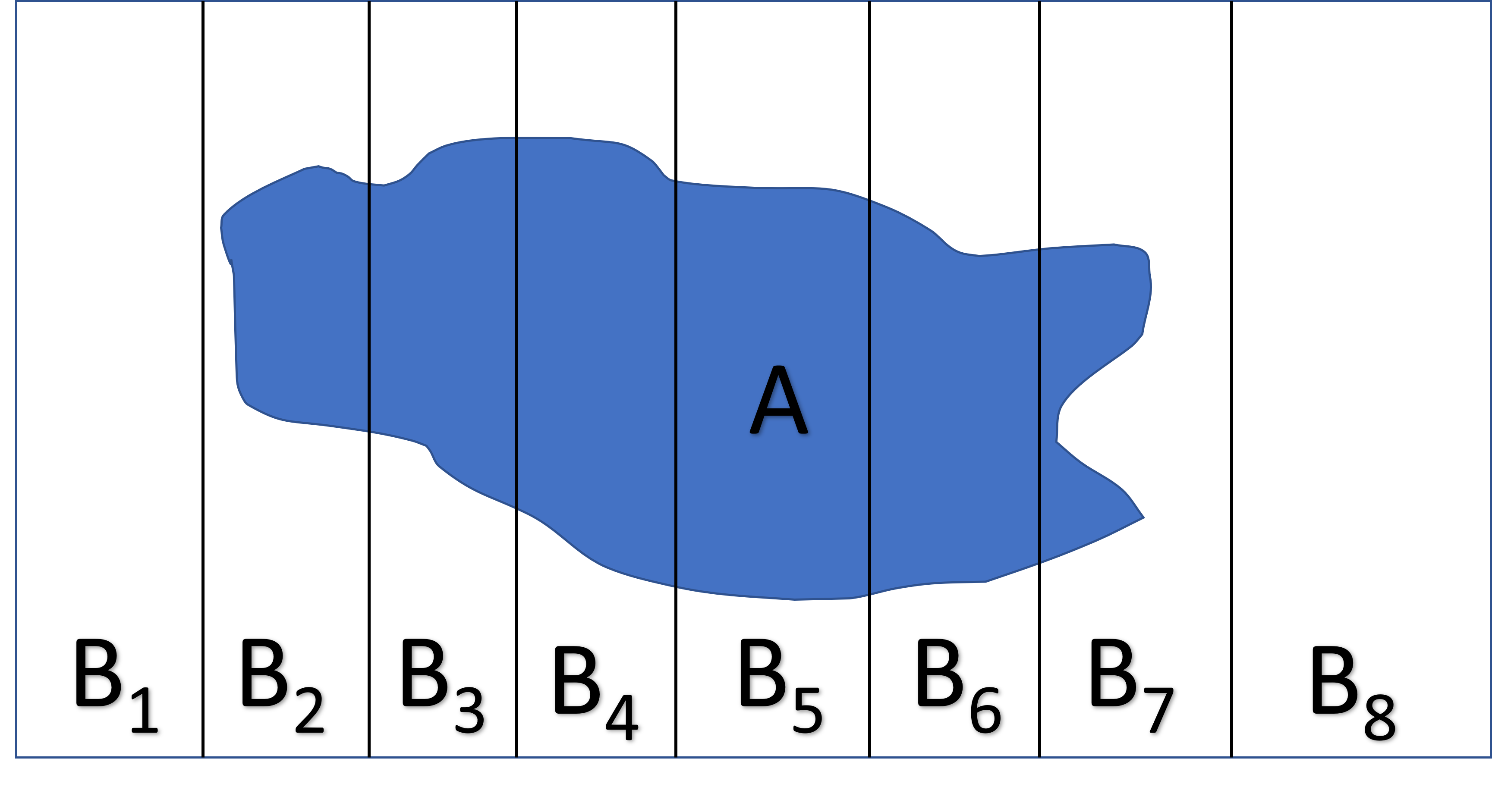
A special case of the total law of probability is:
Lastly, we can combine several of these probability rules to form Bayes Theorem:
We can also write Bayes rule more generally as:
9.2.1 Application of Bayes theorem to diagnostic screening tests
Bayes theorem is the foundation of Bayesian statistics, but it is also often used for frequentist inference, for example, to understand results of various diagnostic tests for which we often have poor intuition (Bramwell, West, and Salmon 2006). As an example, consider the following question posed by Bramwell, West, and Salmon (2006):
The serum test screens pregnant women for babies with Down’s syndrome. The test is a very good one, but not perfect. Roughly 1% of babies have Down’s syndrome. If the baby has Down’s syndrome, there is a 90% chance that the result will be positive. If the baby is unaffected, there is still a 1% chance that the result will be positive. A pregnant woman has been tested and the result is positive. What is the chance that her baby actually has Down’s syndrome?
The answer, using the information above, is
The 1% prevalence rate assumed by Bramwell, West, and Salmon (2006) is close to what the CDC reports for women that are 40 years old or older. The prevalence rate in the general population is actually much lower (closer to 0.1%). As a result, the probability that a baby has Down’s syndrome given that a younger mother receives a positive test is actually much lower than 48%. Let’s repeat the analysis with the lower prevalence rate of 0.1%.
Let:
Our goal is to use Bayes’ theorem to calculate the probability a baby will have Down’s syndrome given that the mother tests positive,
Thus, we need the following:
Plugging these values in to Equation 9.4, we get:
Although this is an order of magnitude larger than the prevalence rate in the population, the probability of the child having Down’s is still low – only 8% – even with a positive test! I remember working through the math when my wife was first pregnant with our oldest child, Zoe, and concluding that we had no interest in the diagnostic test. Many diagnostic tests suffer a similar same fate when prevalence rates in the population are really low.

9.2.2 Bayes rule and problems with multiple testing
Another really useful application of Bayes rule is in understanding problems associated with conducting multiple null hypothesis tests, particularly when hypotheses do not have strong a priori support or when the tests have low power (i.e., probability of detecting an effect when one exists). Let’s consider a scenario in which we test 1000 hypotheses. Assume:
- 10% of the hypotheses are truly false,
- We have an 80% chance of rejecting the hypothesis given that it is false,
- We use an
Given these assumptions, we should expect to report a total of 125 significant findings, but 36% of these significant findings will be incorrect (i.e., rejections when the null hypothesis is true); 64% will be correct. We can use Bayes rule to verify this result. Let’s calculate the probability the null hypothesis is false, given that we rejected it:
Ioannidis (2005) used this framework to explain why studies that attempt to replicate research findings so often fail. The situation may be even worse in ecology, given that the power of most ecological studies is well below 80% and often closer to 20% (see Forstmeier, Wagenmakers, and Parker 2017 and references therein). If we repeat the above calculations but for studies with only 20% power, we find
9.3 Probability Trees
When working through compound probabilities (i.e., probabilities associated with 2 or more independent events), it can often be useful to draw a tree diagram that outlines all of the different possibilities calculated by repeatedly applying the conditional probability rule,

9.3.1 Just for fun: Monte Hall problem
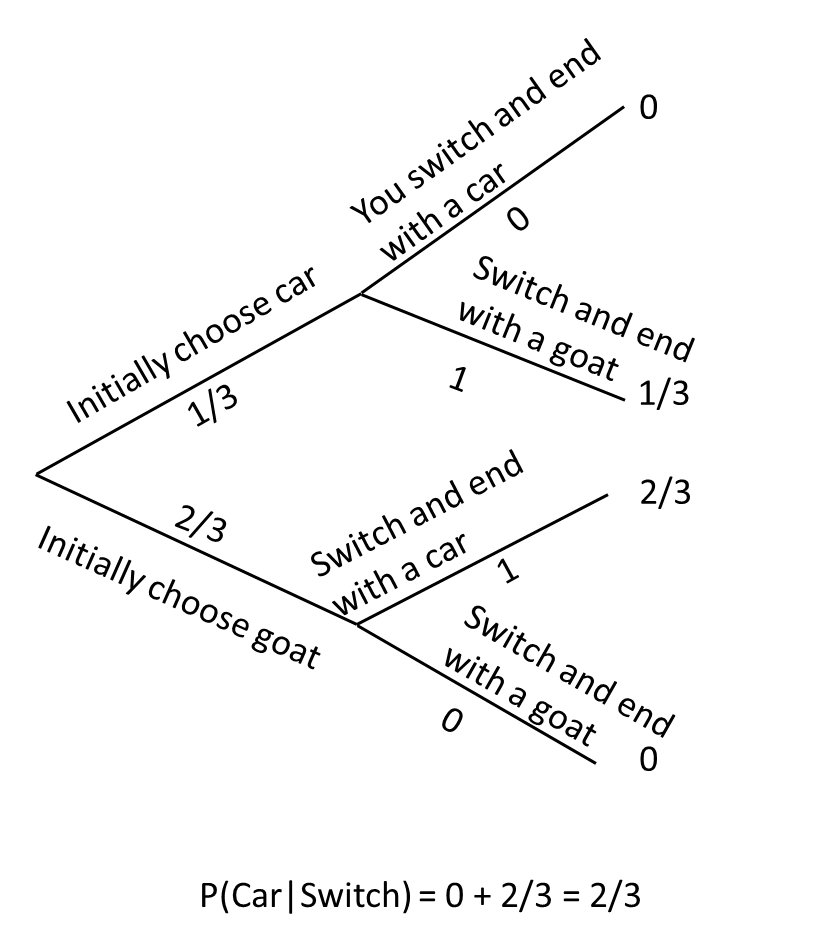
Many of you may have seen a version of the Monte Hall problem before. One of the main reasons I like this problem is that, like the diagnostic testing problem, it can highlight how poor our intuition is at times when working with probabilities. The problem goes like this: suppose you are on a game show where the host asks you to choose from one of 3 doors. Behind one of the doors is a brand new car. Behind the other two are a goat. You are asked to choose a door (if you select the door with the car, you win the car). After you reveal your choice, the host opens one of the doors that you did not choose and shows you a goat. The game show host then asks whether you want to change your initial decision. If you are like most people, you will likely stick with your initial choice, thinking that you have a 50-50 chance of winning either way. But, it turns out that you increase your chances of winning by switching doors. If you switch, you have a 2/3 chance of winning versus 1/3 if you stick with your initial choice!
One way to understand this result is to construct a probability tree representing the initial event (choosing a door with or without a goat) and then the final outcome, conditional on your initial choice and whether you choose to change your decision or not after seeing the game show host reveal one of the 2 goats. If you initially chose a door with a goat, then you will end up with the car if you switch doors. If you initially chose the door with the car, then you will end up with a goat if you switch. The thing is, you are more likely to initially choose a door with a goat than the door with the car. So, in the end, you are best off switching doors once you can eliminate the door where the goat has been revealed.
If this result is surprising to you, you are not alone. For a really interesting read that highlights just how many (mostly overconfident male) PhD scientists not only got this answer wrong, but also choose to publicly deride Marilyn vos Savant (better known for her “Ask Marilyn” column in Parade Magazine) for providing the correct answer see this aticle. You might also be interested in knowing that pigeons (Columba livia) have performed better than humans at solving the Monte Hall problem (Herbranson and Schroeder 2010)!
9.4 Sample space, random variables, probability distributions
In frequentist statistics, probabilities are defined in terms of frequencies of events. Specifically, the probability of event A,
A key consideration is whether we are interested in modeling the distribution of a discrete or continuous random variable. Discrete variables take on a finite or countably infinite number of values1. Examples include:
- age classes = (fawn, adult)
- the number of birds counted along a transect
- whether or not a moose calf survives its first year
- the number of species counted on a beach in the Netherlands
Continuous variables, by contrast, can take on any real number. Examples include:
- (lat, long) coordinates of species in an INaturalist database
- the age at which a randomly selected adult white-tailed deer dies
- mercury level (ppm) in a randomly chosen walleye from Lake Mille Lacs
9.4.1 Discrete random variables
Discrete random variables are easier to consider than continuous random variables because we can directly map events to probabilities. Let’s consider a specific example. Consider sampling 2 white-tailed deer for chronic wasting disease. Assume our 2 individuals are randomly chosen from a population where the prevalence rate of chronic wasting disease is
In this case, the possible events are: (-, -), (-, +), (+, -), (+, +). We could define a random variable,
We next define a probability mass function,
These probabilities can be easily derived by noting the probability of a positive test is
9.4.2 Continuous random variables
For continuous random variables, there are an infinite number of values that
You may recall from calculus that integrating
A few other things to note about continuous random variables are:
- The probability associated with any point is 0;
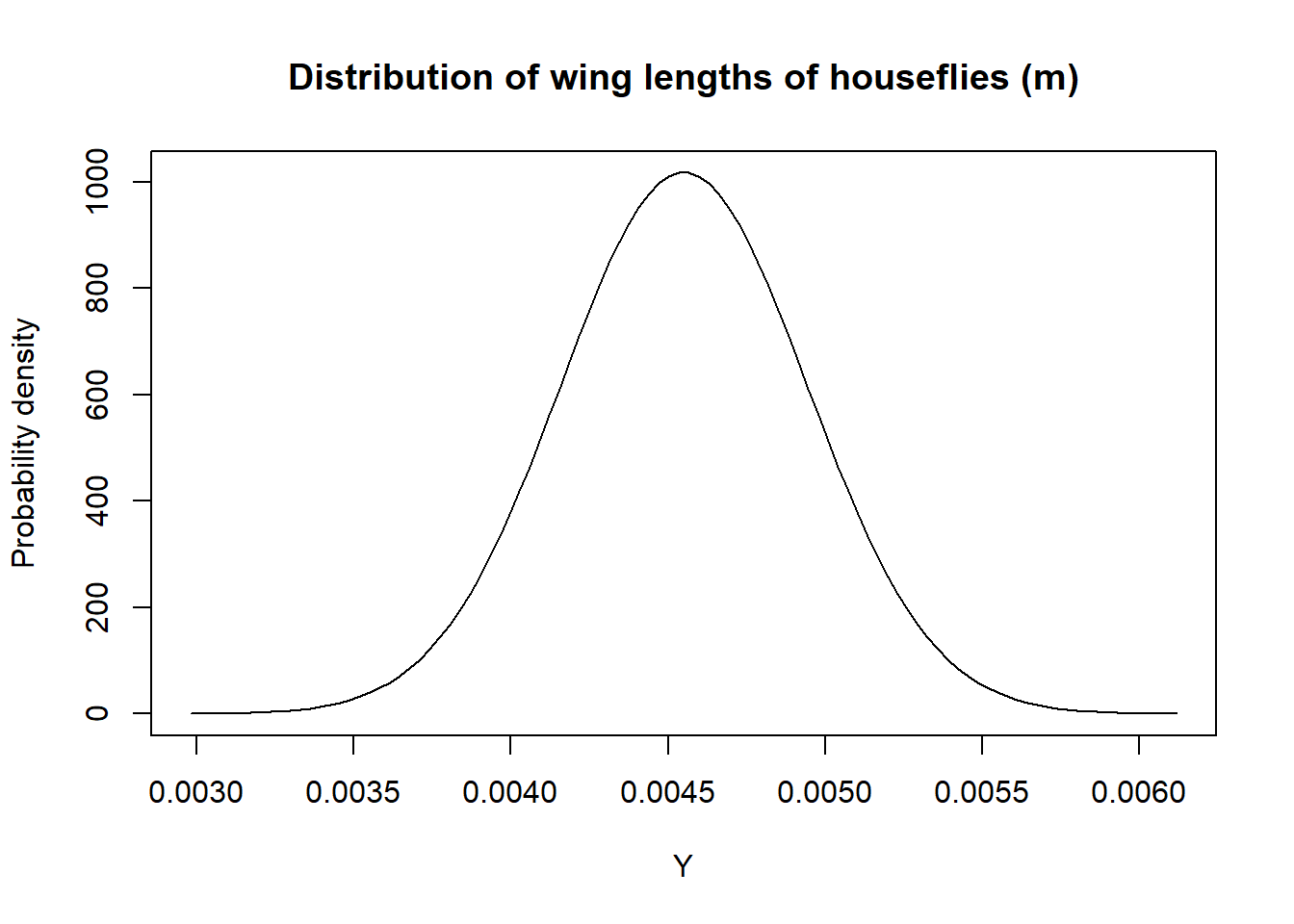
Also, note that unlike probability mass functions, probability density functions can take on values greater than 1. To understand why this must be the case, consider representing the distribution of wing-lengths of houseflies in meters using a Normal distribution with mean = 0.00455 m and standard deviation = 0.000392 m. The range of wing-lengths is much less than 1, so the probability density function must be much greater than 1 for many values of
9.5 Cumulative distribution functions
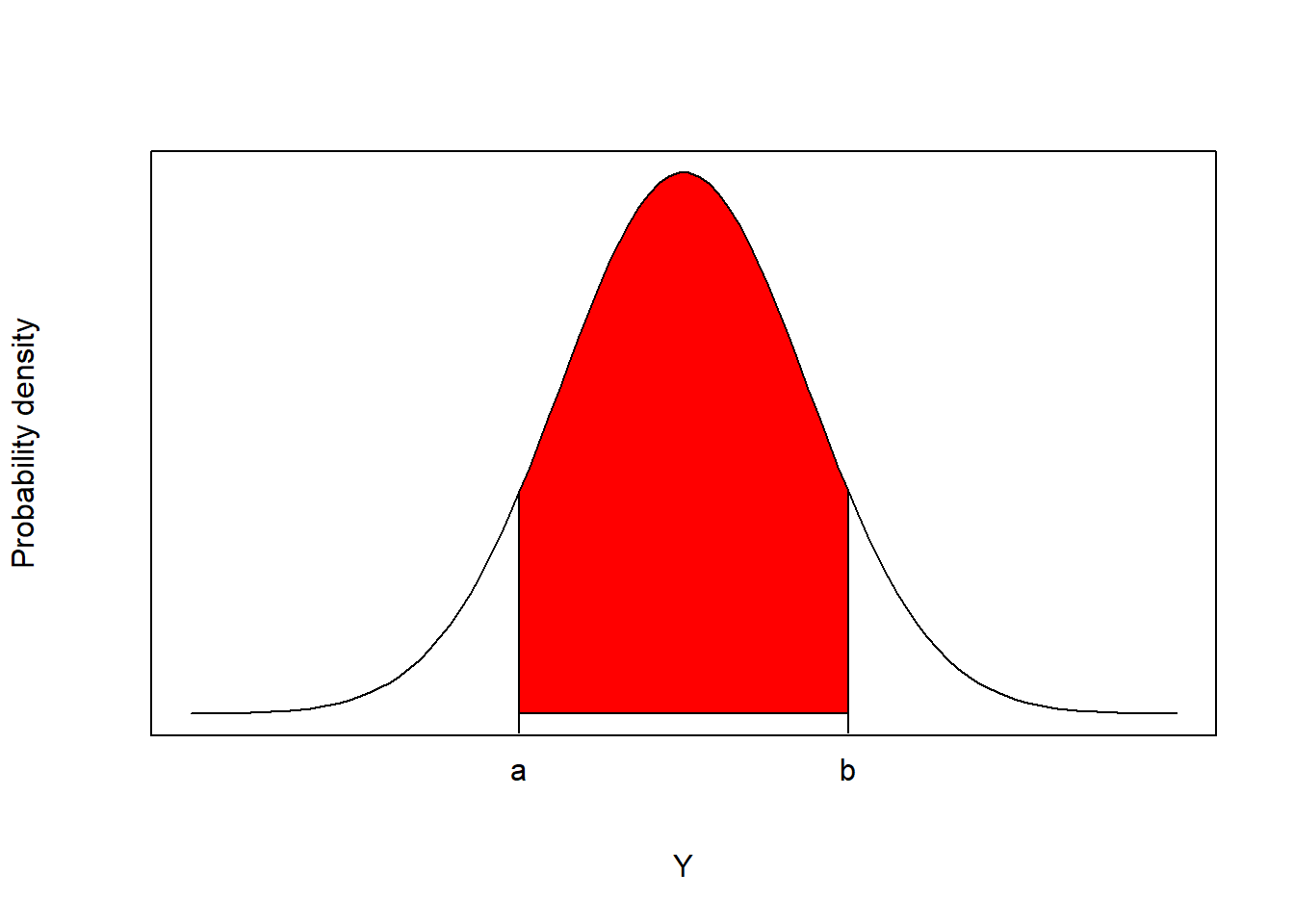
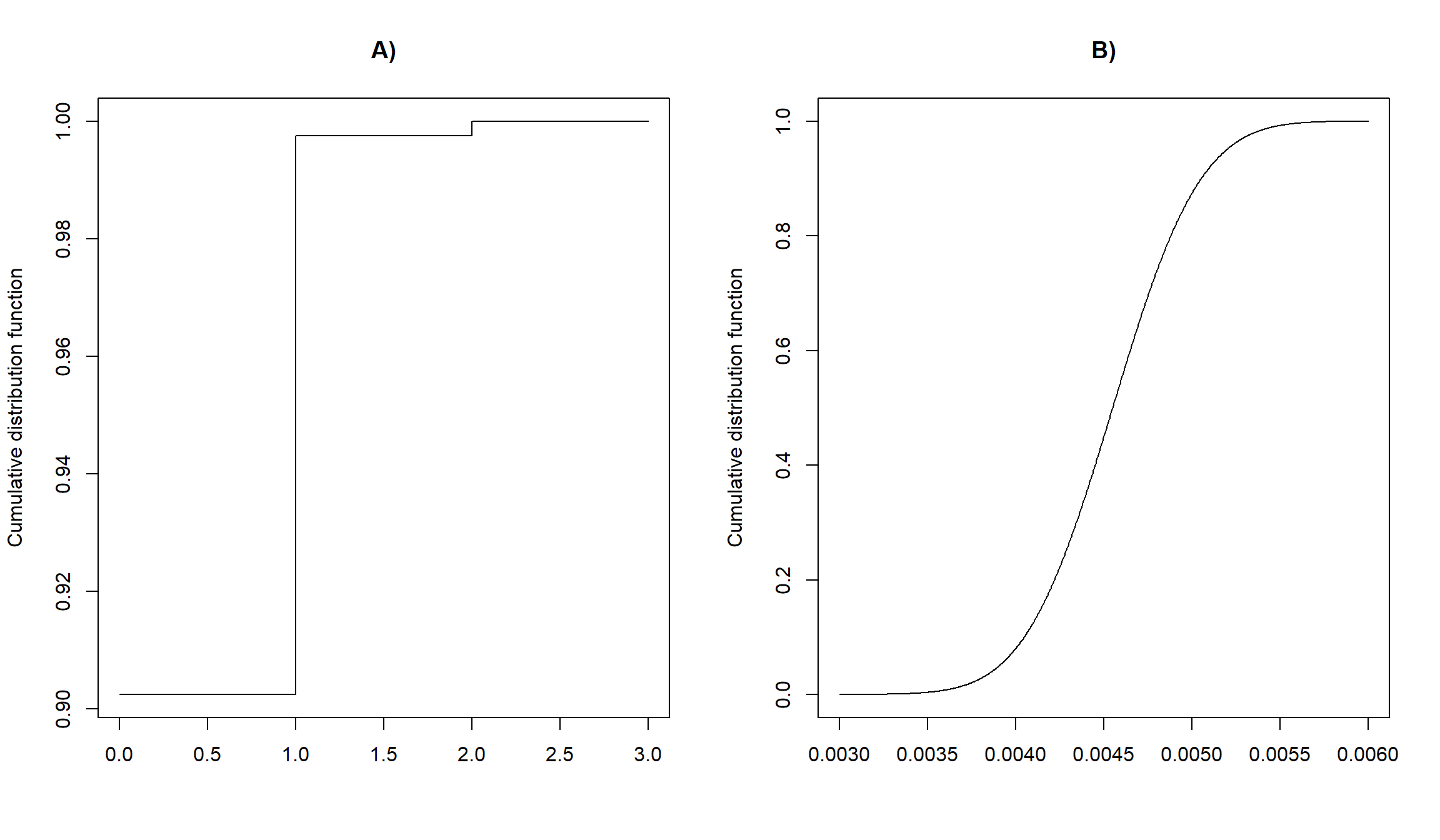
We will often want to determine
The cumulative distribution functions for our chronic wasting disease example assuming
9.6 Expected value and variance of a random variable
For Discrete random variables, we define the expected value and variance as:
For continuous random variables, we define the expected value and variance as:
The expected value gives the average value you would see if you generated a large number of random values from the probability distribution. Also, note that the standard deviation of a random variable is equal to
Example: Let’s calculate the mean and variance of our random variable describing the number of positive tests for chronic wasting disease when sampling 2 random deer:
Deriving the final expression for the variance requires a lot of algebra (but, can be simplified using online calculators – e.g., here). Note, it is often easier to derive the variance using an alternative formula:
If you were to take a mathematical statistics course, you would likely derive this alternative expression for the variance and also derive expressions for the mean and variance associated with several common probability distributions.
9.7 Expected value and variance of sums and products
We will often need to calculate the expected value or variance of a sum or product of random variables. For example, in Section 3.12, we needed to be able to determine the variance of a sum of regression parameter estimates when calculating the uncertainty associated with pairwise differences between means for different values of a categorical variable. Similarly, in Chapter 5, we needed to calculate the mean and variance for a linear combination of our regression parameters in order to plot
- If
9.8 Joint, marginal, and conditional distributions
There are many situations where we may be interested in considering more than 1 random variable at a time. In these situations, we may consider:
- joint probability distributions describing probabilities associated with all random variables simultaneously.
- conditional distributions describing probabilities for one or more of the random variables, given a realization of the other random variables.
- marginal distributions describing the probability of one of the random variables, which can be determined by averaging over all possible values of the other random variables.
Again, these concepts are easiest to understand when modeling discrete random variables since we can use a joint probability mass function to assign probabilities directly to unique combinations of the values associated with the two random variables. Consider the following simple example with two random variables,
We will assume that the probability that a randomly chosen site is occupied by the species of interest is given by
We will further assume that the probability that a species is detected at a randomly chosen site is equal to
when
when
Joint distribution from a conditional and marginal distribution
We can derive the joint probability mass function for
We can verify that this is a valid joint probability distribution by noting that
Marginal distribution from the joint distribution
We can derive the marginal probability mass function of
Conditional distribution from the joint and marginal distribution
We can then derive the distribution of
Importantly, this provides us with an estimate of the probability a site is occupied given that we did not detect the species at the site. The conditional distribution when
For continuous distributions, we can replace sums with integrals to specify relationships between joint, conditional, and marginal probability density functions:
These concepts are critical for deriving appropriate Monte Carol Markov Chain (MCMC) algorithms when fitting models in a Bayesian framework, and they are relevant to many of the models that are popular among ecologists, some of which we will explore in later chapters:
Models with random effects (Chapter 18 and Section 19.5). We will specify these models in terms of a distribution of a response variable conditional on a set of random effects along with a distribution of the random effects.
Models with latent (unobserved) variables, including occupancy models (MacKenzie et al. 2017). Models for Zero-inflated data (Chapter 17) can also be formulated in terms of a latent variable.
When fitting models with random effects or other latent variables in a frequentist framework, we must first derive (or approximate) the marginal distribution of the response variable after integrating or summing over the possible values of the unobserved random variables. Although we do not have to derive the marginal distribution of the response variable when fitting similar models in a Bayesian framework, doing so will often help speed up the model fitting process (Ponisio et al. 2020; Yackulic et al. 2020, see also this blog)).
Think-pair-share: explain why Bill Gate’s reasoning is flawed in Figure 9.10 (thanks to Richard McElreath for tweeting this out!):
9.9 Probability distributions in R
This section closely follows Jack Weiss’s lecture notes from his various classes. There are 4 basic probability functions associated with each probability distribution in R. These functions start with either - d, p, q, or r - and are then followed by a shortened name that identifies the distribution :
d is for density and returns the value of f(y), i.e., the value of the probability density function (continuous distributions) or probability mass function (discrete distributions).
p is for probability; returns a value of F(y), the cumulative distribution function.
q is for quantile; returns a value from the inverse of F(y) and is also known as the quantile function.
r is for random; generates a random value from the given distribution.
Let’s consider these 4 functions in the context of the Normal distribution with mean 0 and standard deviation 1. The functions are named dnorm, pnorm, qnorm, rnorm and are depicted in Figure 9.11.
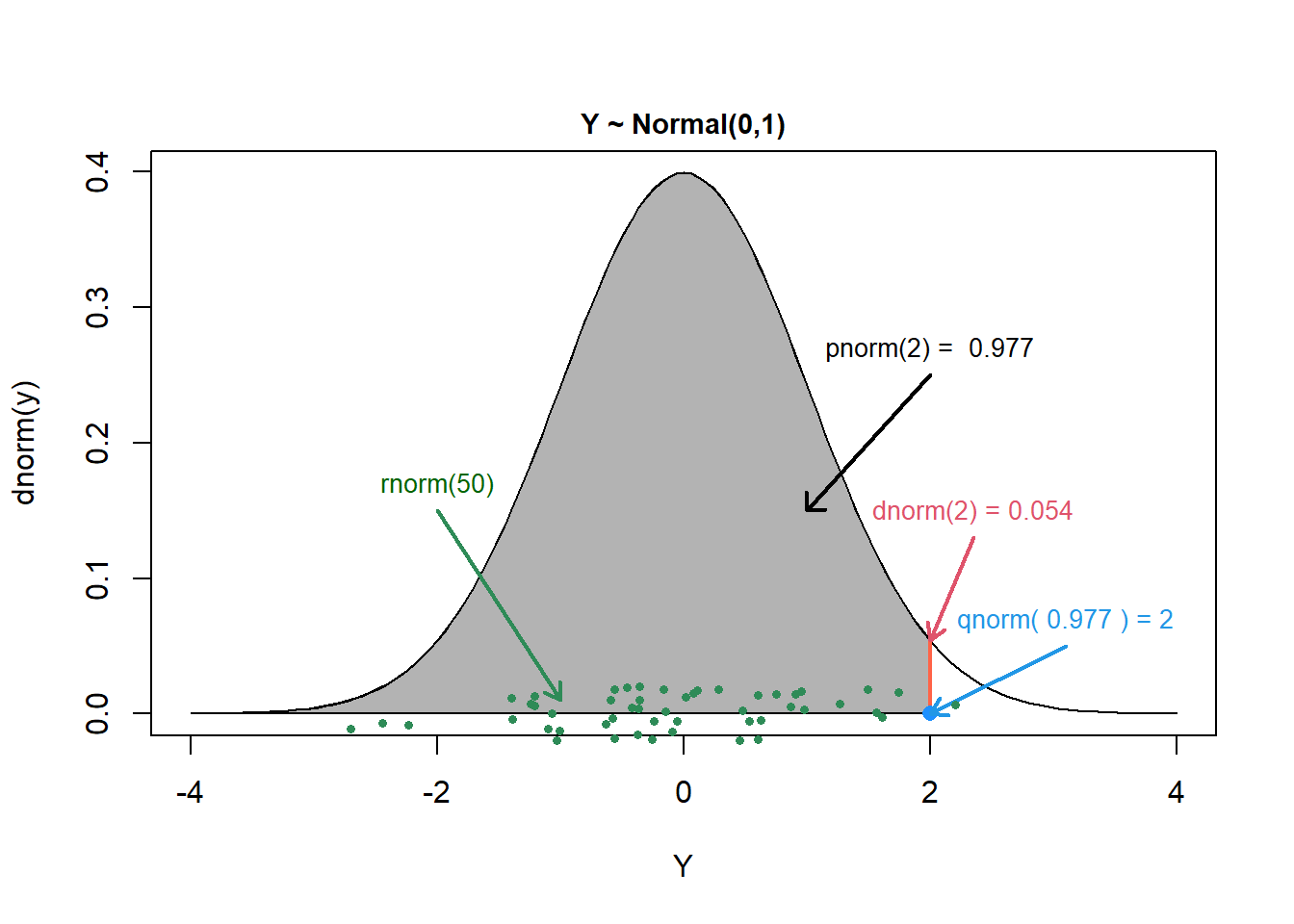
dnorm(2)2 or returns the value of the probability density function at
pnorm(2) returns the value of the cumulative distribution function,
qnorm(0.977 returns the quantile function and determines the value of
rnorm(50) generates 50 random values from a standard normal distribution, represented by the green points in Figure 9.11.
9.10 A sampling of discrete random variables
In the next few sections, we will consider several discrete and continuous probability distributions that are commonly used to model data or to test hypotheses in statistics.
9.10.1 Bernoulli distribution:
The Bernoulli distribution is used to model discrete random variables that can take on only two possible values, 1 or 0, with probabilities
Characteristics:
- Parameter:
- Support (i.e., range of values that
- R does not contain functions specific to the Bernoulli distribution; rather, we have to work with functions for the Binomial distribution, which we will see next.
- JAGS and WinBugs: dbern
9.10.2 Binomial distribution
A binomial random variable counts the the number of successes in a set of
then,
The combinatoric term,
In our chronic wasting disease testing example (with
Characteristics:
- Typically, the number of trials is assumed fixed and known, leaving a single parameter
- Support:
- R: dbinom, pbinom, qbinom, rbinom with arguments
size=prob= - JAGS: dbin(p, n)
Uses: a Bernoulli or binomial distribution is often used to model presence/absence and detection/non-detection data from wildlife surveys. It can also be used to model survival (Y/N), the number of eggs in a clutch that will hatch (or number of chicks that will fledge), etc.
Example: Raymond Felton, a point guard on the University of North Carolina’s 2005 National Championship team, shot free throws at a 70% success rate during the 2004-2005 season. If we assume each of his free throw attempts can be modeled as independent trials, what is the probability that he would hit at least 4 out of 6 free throws in the 2005 Championship Game (he hit 5)?3
There are several ways to compute this probability in R:
- Using
choose(6,4)*(0.7)^4*(0.3)^2 +
choose(6,5)*(0.7)^5*(0.3) +
0.7^6[1] 0.74431- Using R’s built in probability mass function,
dbinom:
sum(dbinom(4:6, size = 6, p = 0.70))[1] 0.74431- Using R’s built in cumulative distribution function,
pbinom, and recognizing that
1- pbinom(3, size = 6, p = 0.7)NA [1] 0.74431- We can also use
pbinomwith the argumentlower.tail = FALSE, which will give us
pbinom(3, size = 6, p = 0.7, lower.tail= FALSE)[1] 0.744319.10.3 Geometric distribution
The Geometric distribution arises from considering the number of failures until you get your first success in a set of Bernoulli random trials. To derive the probability mass function for the Geometric distribution, note that we have to have
- Parameter:
- Support:
- R: *geom with parameter
prob= - JAGS: dnegbin(p, 1)
Other notes:
Sometimes the Geometric distribution is defined as the number of trials until the first success. In this case, the probability mass function is defined as:
with support:
9.10.4 Multinomial distribution
The multinomial distribution is a generalization of the binomial distribution, allowing for
Characteristics:
- Parameters:
- R: dmultinom, pmultinom, qmultinom, rmultinom with parameters
size=prob= - JAGS: dmulti(p,n)
Uses:
The multinomial distribution is often appropriate for modeling a categorical response variable with more than 2 unordered categories. The multinomial distribution frequently arises when modeling capture histories in mark-recapture studies (e.g., Otis et al. 1978; Pollock et al. 1990).
9.10.5 Poisson distribution:
The Poisson distribution is often used to model counts of events randomly distributed in space or time, occurring at a rate,
Similarly, let
Oftentimes, observations are recorded over constant time intervals or spatial units all of the same size. In this case, the probability mass function would be defined simply as:
Characteristics:
- Parameter:
- Support:
- R: dpois, ppois, qpois, and rpois with parameter
lambda. - JAGS: dpois(lambda)
Uses: the Poisson distribution is often used as a null model in spatial statistics. Although it can be used as a general model for count data, most ecological data are “overdispersed”, meaning that
Example: suppose a flower bed receives, on average, 10 visits by Monarchs a day in mid-August. Further, assume the number of daily visits closely follows a Poisson distribution. What is the probability of seeing 15 monarchs on a random visit to the garden?
dpois(15, lambda=10)[1] 0.0347180710^15*exp(-10)/(factorial(15)) [1] 0.034718079.10.6 Negative Binomial
9.10.6.1 Classic parameterization
There are 2 different parameterizations of the Negative Binomial distribution, which we will refer to as the “classic” and “ecological” parameterizations. Consider again a set of independent Bernoulli trials. Let
- We will have a total of
- The last trial will be a success (with probability
- The preceding
Characteristics:
- Parameters: r must be integer valued and > 0,
- Support:
- In R: *nbinom, with parameters (
prob= p,size=
9.10.6.2 Ecological parameterization
To derive the ecological parameterization of the Negative Binomial distribution, we express
Plugging these values in to
Then, let
Characteristics:
- Parameters:
- in R: *nbinom, with parameters
mu=size= - JAGS: dnegbin with parameters (
Uses: the Negative Binomial model is often used to model overdispersed count data where the variance is greater than the mean. Note that as
Other notes: if
9.11 A sampling of continuous probability distributions
9.11.1 Normal Distribution
The probability density function for the normal distribution is given by:
Characteristics:
- Parameters:
- Support:
- R: dnorm, pnorm, qnorm, rnorm; these functions have arguments for the
meanand standard deviation,sd, of the Normal distribution - JAGS: also has a dnorm function, but it is specified in terms of the precision,
Uses: the Normal distribution forms the backbone of linear regression. The Central Limit Theorem tells us that as
Other notes: one of the really unique characteristics of the Normal distribution is that the mean and variance are independent (knowing the mean tells us nothing about the variance and vice versa). By contrast, most other probability distributions have parameters that influence both the mean and variance (e.g., the mean and variance of a binomial random variable are
Special cases: setting
9.11.2 log-normal Distribution:
Characteristics:
- Parameters:
- Support:
- R: dlnorm, plnorm, qlnorm, rlnorm with parameters
meanlogandsdlog - JAGS: dlnorm(meanlog, 1/varlog)
Uses: whereas the Normal distribution provides a reasonable model for response variables formed by adding many different factors together, the lognormal distribution serves as a useful model for response variables formed by multiplying many independent factors together. This follows again from the Central Limit Theorem since
9.11.3 Continuous Uniform distribution:
If observations are equally likely within an interval
Characteristics:
- Parameters:
- R: *unif with
min= a,max= b - JAGS: dunif(lower, upper)
Uses: the uniform distribution is often used as a model of ignorance for prior distributions. Also, p-values across replicated experiments in which the null hypothesis is true should follow a uniform distribution.
9.11.4 Beta Distribution:
The Beta distribution is unique in that it has support only on the (0,1) interval, which makes it useful for modeling probabilities (or as a prior distribution for
This is the first time we have seen the gamma function (
The gamma function generalizes factorials (gamma(n), e.g., gamma(4) = 3! =
gamma(4)[1] 6Characteristics:
- Parameters:
- Support:
- R: *beta with
shape1=shape2= - JAGS: dbeta
Uses: the Beta distribution is sometimes used to model probabilities or proportions (in cases where the number of trials is not known). It is also frequently used as a prior distribution for
Special cases: when
9.11.5 Exponential:
If we have a random (Poisson) event process with rate parameter,
Characteristics:
- Parameter:
- Support:
- R: *exp with
rate= - JAGS: dexp
Uses: often used to model right-skewed distributions, particularly in time-to-event models.
9.11.6 Gamma Distribution:
If we have a random (Poisson) event process with rate parameter,
- Parameters:
- Support:
- R: *gamma with
shape=rate=shape=scale= - JAGS: dgamma(alpha, beta)
Uses: the Gamma distribution can be used to model non-negative continuous random variables. In movement ecology, the Gamma distribution is often used to model step-lengths connecting consecutive telemetry locations
Special cases: when
9.12 Some probability distributions used for hypotheses testing
9.12.1
The
The probability density function for the
Characteristics:
- Parameter:
- Support:
- R: *chisq with
df= - JAGS: dchisqr(k)
9.12.2 Student’s t distribution
We encountered the t-distribution in Chapter 1, which we used to test hypotheses involving individual coefficients in our regression models. The probability density function for the student t distribution with
Characteristics:
- Parameter:
- Support:
- R: *t with
df=ncp= non-centrality parameter - JAGS: dt(mu, tau, k), with
tau=1, thenmuis equal to the non-centrality parameter in R andkis the degrees of freedom
9.12.3 F distribution,
We saw the F-distribution when testing whether multiple coefficients associated with a categorical predictor were simultaneously 0 in Section 3.10. The probability density function for the F-distribution with
Characteristics:
- Parameter:
- Support:
- R: *f with
df1=df2=ncp= non-centrality parameter - JAGS: df
9.13 Choosing an appropriate distribution
How do we choose an appropriate distribution for our data? This may seem like a difficult task after having just been introduced to so many new statistical distributions. In reality, you can usually whittle down your choices to a few different distributions by just considering the range of observations and the support of available distributions. For example:
- If your data are continuous and can take on any value between
- If your data are continuous, non-negative, and right-skewed, then a log-normal or gamma distribution is likely appropriate; if your data also contain zeros, then you may need to consider a mixture distribution (see Chapter 17).
- If you are modeling binary data that can take on only 1 of 2 values (e.g., alive/dead, present/absent, infected/not-infected), then a Bernoulli distribution is appropriate.
- If you have a count associated with a fixed number of “trials” (e.g.,
- If you have counts associated with temporal or spatial units, then you might consider the Poisson or Negative Binomial distributions (or zero-inflated versions that we will see later).
- If you are modeling time-to-event data (e.g., as when conducting a survival analysis), then you might consider the exponential distribution, gamma distribution, or a generalization of the gamma called the Weibull distribution.
- If you have circular data (e.g., your response is an angle or a time between 0 and 24 hours or 0 and 365 days), then you would likely want to consider specific distributions that allow for periodicities (e.g., 0 is the same as 2
9.14 Summary of statistical distributions
You may find it useful to visualize different statistical distributions. This site is great! You can choose from many different statistical distributions and vary their parameters to see how it changes the probability (mass or density) function and the cumulative density function! Thanks to Jeremiah Shrovnal for pointing me to it!
Table 9.2 briefly details most of the random variables discussed in this chapter and was modified from this site.
| Distribution Name | pmf / pdf | Parameters | Possible Y Values | Description |
|---|---|---|---|---|
| Bernouli | Success or failure | |||
| Binomial | Number of successes after |
|||
| Geometric | Number of failures until the first success | |||
| Multinomial | Number of successes associated with each of |
|||
| Poisson | Number of events in a fixed time interval or spatial unit | |||
| Negative Binomial (classic) | Number of failures before |
|||
| Negative Binomial (ecological) | A model for overdispersed counts | |||
| Normal | Model for when a large number of factors act in an additive way | |||
| log-Normal | Model for when a large number of factors act in an multiplicative way | |||
| Uniform | Useful for specifying vague priors | |||
| Beta | Useful for modeling probabilities | |||
| Exponential | Wait time for one event in a Poisson process | |||
| Gamma | Wait time for |
|||
| Distribution for goodness-of-fit tests, likelihood ratio test | ||||
| Students t | Distribution for testing hypotheses involving means, regression coefficients | |||
| F | Distribution for testing hypotheses involving regression coefficients |
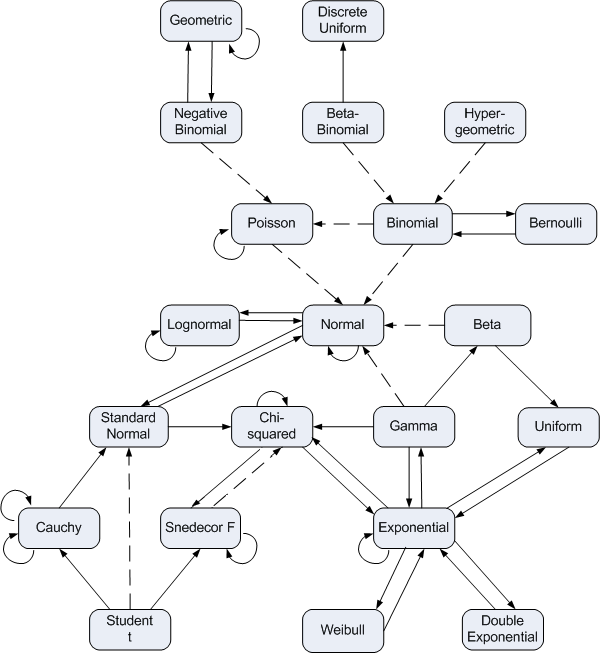
In a few places, we have highlighted connections among different statistical distributions, but there are many other connections that we did not mention (e.g., see Figure 9.13).
9.15 References
A countably infinite set of values can be put in a 1-1 correspondence with the set of non-negative integers.↩︎
Note, we have ignored the other arguments to this function, which include
meanandsd, allowing them to take on their default values of 0 and 1.↩︎I became a huge University of North Carolina basketball fan after going to graduate school in Chapel Hill and attending nearly every home basketball game for 6 years. My son is named after Raymond Felton, the point guard from the 2005 National Championship team and my youngest daughter is named Carolina Anne. I had plane tickets to join friends of mine in Chapel Hill to watch the 2005 Championship game, but ultimately decided not to go. My oldest daughter, Zoe, was only 2 weeks old. I had also witnessed 4 final four losses during my time in North Carolina. Ultimately, I decided to watch the game with my wife and daughter at home.↩︎
Once we know